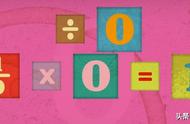自从我们开始学习数学以来,我们就习惯于将某个数除以另一个数或同一个数。这没什么大不了的。但这里有一件大事,我们总是被警告,即,将任何数字除以零 (0)。但为什么?因为当你这样做时你会得到无穷大。但是,当我们将任何数字除以零时,我们如何以及为什么倾向于得到这样的结果呢?

让我们看一下,以便更好地理解!!!
▪ 首先,什么是乘法?无非就是重复加法。
示例:2×3=6 这意味着我们需要将 2 加三次才能得到 6。
▪ 其次,什么是除法?除非我们得到零,否则只能重复减法。
示例:15/5=3 表示 15 减去 5 三次得到 0。即 15–5–5–5=0
但是让我们检查一下 1/0 的情况。根据上面所示的除法理论,我们需要找出需要从 1 中减去 0 的次数。
即,1/0=1–0–0–0–0–0–0-………………..
呃哦,看起来这会一直持续下去(无限次)但是我们仍然不知道需要从 1 中减去多少个 0 才能使结果为 0。所以简单地说,我们不能在中定义 1/0正常除法项,因此未定义。
换句话说,这里我们无法找到应该减去的零的极限。因此,1/0 可以被认为是未定义的。
现在清了吗???如果没有,让我们看看另一种方法。
让我们通过减小分母的值来对相同的数字进行简单的除法!!!
1/1=1, 1/0.1=10, 1/0.01=100, 1/0.001=1000, 1/0.0001=10000 这里,当我们减小分母的值时,表达式的值继续增加。因此,当分母的值趋于或等于零时,表达式的值趋于或变得如此之大以至于我们找不到它的界限,或者在其他情况下它变为无穷大,即 1/0=∞。
清晰简单!是的?但是等等,这里有一个大问题。现在,那是什么?
在这里,我们只对一个数字“1”进行了除法程序。让我们检查'2'。
2/1=2, 2/0.1=20, 2/0.01=200, 2/0.001=2000, 2/0.0001=20000 同上,数值继续增加。将 2 除以 0,我们得到无穷大,即 2/0=∞
0 上的 1 和 0 上的 2 都等于无穷大 (∞) 是不是有点令人难以置信?
因此,根据上述结果,1/0=2/0 并且根据基本数学规则,我们可以写出 1=2,这在数学上和逻辑上都是不正确的。1≠2。
因此,它变得更加复杂,最后我们得出结论,任何除以零的数字都是不确定的。
谢谢你!