晓查 发自 凹非寺
量子位 报道 | 公众号 QbitAI
你在看到标题的时候,一定会想:
这个问题我知道答案:x、y、z都等于1。
如果再多算几步,你还能发现4、4、-5也是一组整数解。

注意审题,以上只是方程x³ y³ z³=3的前两组整数解,第3组整数解是多少,你知道吗?
1953年,数学家Louis Mordell提出一个疑问:这个第3组整数解,它存在吗?
最近,这组解终于被找到了。
警告一下,千万别尝试用穷举法编程!
因为这3个数远远超出了长整型的范围,但数学家还是动用了40万台电脑把答案找出来了。
另外,这两位数学家还把程序代码开源了。

当然,他们并非暴力搜索。这时候数学的作用就来了:它能为你提供算法,告诉你搜索范围,大大缩小搜索空间。
一个正整数能否表示成三个整数的立方之和(x³ y³ z³=k),关于它的每次发现都能引起不小的轰动。
这个看似没技术含量的问题,其实困扰了数学界很久。
三个立方数之和1992年,数学家Roger Heath-Brown提出了一个猜想:对于一个正整数k,如果它除以9的余数不是4或5(k不等于9n±4),那么k就可以表示成三个整数的立方之和。
而且每个k都有无穷多组整数解。
对于k小于100的情况,2019年之前只有k=33、42没有找到整数解。
2019年3月,33告破:
33 = 8866128975287528³ (-8778405442862239)³ (-2736111468807040)³
2019年9月,麻省理工的Andrew Sutherland和布里斯托大学Andrew Booker的两位安德鲁找到了42的答案:
42 = (-80538738812075974)³ 80435758145817515³ 12602123297335631³
当时,菲尔兹奖得主、剑桥大学教授Timothy Gowers还转推“祝贺”。
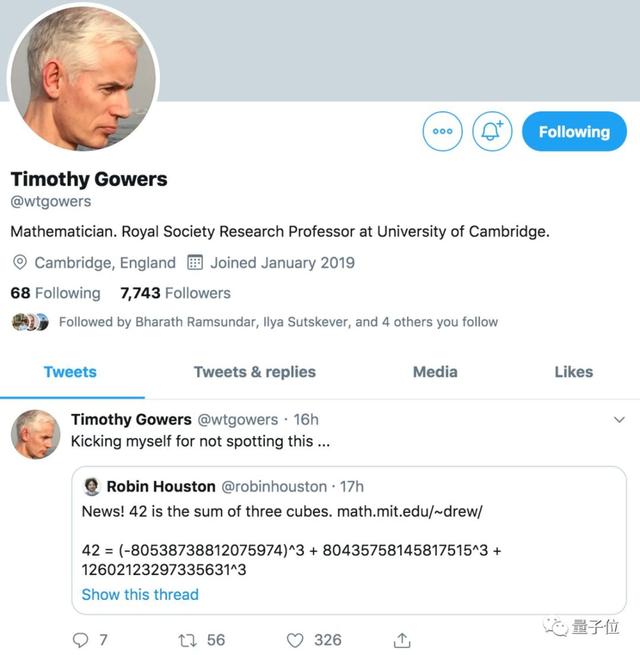
虽然100以内的数皆告破,但几十年间却没有关于k=3的新解,许多人开始相信这个所谓的新解根本不存在,Heath-Brown猜想也是错的。
但是,在找到42的答案之后,这两位安德鲁很快就出乎意料找到了k=3的第三组整数解:
数学化简3 = 569936821221962380720³ (-569936821113563493509)³ (-472715493453327032)³
为了找到42和3的解决方案,两位数学家从现有算法开始,将立方和公式转化为他们认为更容易求解的形式: