有关三角形知识点的理解和运用
‘

概念理解1:三角形是由三条线段围成的图形。在这里,“围成”是指首尾相接的意思,不能把“围成”改成“组成”。三角形都有3条边,3个角,3个顶点并且都可以画三条高。
概念理解2:三角形的内角和都是180°。也就是说,三角形的内角和与它的大小、类型都没有关系,只要是三角形内角和都是180°。如:1把一个大三角形沿高剪成两个小三角形或把两个小三角形拼成一个大三角形,它们的内角和也都是180°。同样用放大镜看一个三角形它的内角和也仍是180°。
2.一个三角形中,最多有3个锐角,至少有2个锐角,最多有1个直角,同样最多有1个钝角。
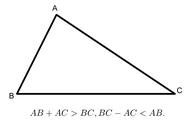
概念理解3:三角形任意两边之和大于第三边,任意两边之差小于第三边。反过来说,即三角形的其中一边小于其它任意两边之和,大于其它任意两边之差。
概念理解4:三角形按角分可以分为:锐角三角形,直角三角形和钝角三角形;按边分有:等腰三角形和等边三角形。
锐角三角形的3个角都是锐角;直角三角形有一个角是直角;钝角三角形有一个角是钝角;等腰三角形的两条边相等,两个底角相等;等边三角形的三条边相等,三个内角相等,都是60度;等边三角形也叫正三角形,它是特殊的等腰三角形,而等腰三角形不一定是等边三角形;等边三角形按角分又是锐角三角形。等腰三角形按角分可能是直角三角形,锐角三角形或钝角三角形。
1,知道一个三角形两个角的度数求第三个角的度数,用180度减去这两个角的度数和。 也 可以用180度连续减去这两个角的度数。
2,知道等腰三角形顶角的度数求底角的度数,用180度减去顶角的差再除以2。即(180°-顶角)÷ 2。如:一个等腰三角形的顶角是100°,一个底角是( 40°),可以用:(180°➖100°)÷2=40°
3,知道等腰三角形底角的度数求顶角的度数,用180度减去底角的2倍。即:180°-底角×2。 如:一个等腰三角形,它的一个底角是45°,则它的顶角是( 90°)。可以用:180°-45°✖️2=90°
4,知道直角三角形的一个锐角求另一个锐角的度数:用180°减去90°再减去所知锐角的度数。即180°-90°-已知锐角度数或90°➖已知锐角度数。如:在一个直角三角形中,其中一个锐角是60°,则另一个锐角是30°,列式为:180°➖90°➖60°=90°➖60°=30°。5,钝角三角形的两个锐角和小于90°,直角三角形的两个锐角和等于90°,锐角三角形任意两个锐角的和都大于90°。等腰直角三角形两个底角都是45°。
及时练习:
填空:1,一个等腰三角形中,顶角是98°,一个底角是( )。
2,在一个直角三角形中角1等于40°,则角2等于( )。(角1和角2是两个锐角)
3,在一个三角形中,其中两个角分别是60°和20°,那么第三个角是( )度,它是一个( )三角形。
4,等腰直角三角形的三个内角的度数分别是( ),( ), ( )。
5,一个等腰三角形,它的一个底角是65°,它的顶角是( )度。
6,在钝角三角形中,两个锐角的和( )90°。(填大于、小于或等于)。
二,判断
1,一个三角形中不可能有两个钝角,但可能有两个直角。( )
2,钝角三角形的内角和大于锐角三角形的内角和。( )
3,把一个大三角形剪成两个小三角形之后,每个小三角形的内角和都是90°。( )
4,用一个放大镜看一个三角形,看到的三角形的内角和是1800°。( )
5,一个三角形中可能有三个锐角。 ( )
6,三角形任意两个内角之和大于第三个内角。 ( )
答案:一:1,41° 2,50° 3,100°,钝角 4,90°,45°,45° 5,50° 6,小于
二:1,╳ 2,╳ 3 ,╳ 4, ╳ 5 ,√ 6,╳