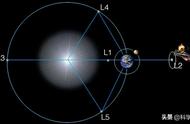
所以我们所说的限制性三体问题仅仅是对物理实际简化的结果,现实生活中是无法用简单的质点来模拟运动的,其额外因素非常多。
太阳系中太阳、地球和月球的运动,科学家就通常将其看作限制性三体问题,这是因为因为太阳的轨道恒定,地球的轨道恒定,地日的关系恒定,将它略去太阳轨道偏心率、太阳视差和月球轨道倾角,将它看成一种特殊的数学模型。从而得到一个周期!

也正因为太阳系中太阳、地球和月球的运动轨迹可循,因此地球才能维持相对恒定的生存环境,这就是我们和三体星的区别。
但是,即使是对这样极度简化的模型,也还是没有解析通解,也就是得到一个普遍适用的公式是不可能的。
为什么会这样呢?因为如果要真正解决三体问题,是要建立一种数学模型,使得在已知任何一个时间断面的初始运动矢量时,能够精确预测三体系统以后的所有运动状态。因为每一个天体在其他两个天体的万有引力作用下的运动方程都可以表示成3个二阶的常微分方程,或6个一阶的常微分方程,而我们只能找到十六个积分,无法求解这个十八阶的微分方程租。

如果我们用现如今最快的计算机模拟三体运动他们的模型是这样的,完全处于混沌状态。

而不同的天体组成“三体问题”,它们的运动轨迹只能一个个去计算,那么它的数值解肯定是会不一样的,而求解过程中的计算会存在误差,但这些微小误差由于互相累积会被极度放大,其结果也是发散的,即可能与实际情况偏差极大。(数值解是在特定条件下通过近似计算得出来的一个数值, 解析解就是表达式中可以算出任何对应值)