正因为我们根本没有办法把所有“三体问题”归纳整理为一个公式,从而得出解析解,所以科学家才会把“三体问题”看作是永远无解的难题。
正是因为三体问题永远无解,所以科学家一般都是研究限制性三体问题的特解。正如我们刚才所说:
限制性三体问题是指在三个天体中,有一个天体的质量为无限小,以至于它的存在不影响另外两个有限质量天体在相互作用下的运动。
后来科学家就把限制性三体问题按有限质量天体的运动轨迹,可以分为圆型限制性三体问题,椭圆型限制性三体问题,抛物线型限制性三体问题。

而其中我们最为熟悉的限制性三体问题的特殊条件解,那就是拉格朗日点。
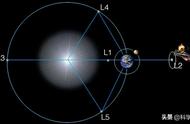
这是1772年,法国数学家、力学家和天文学家拉格朗日,他发表了一篇关于“三体问题”的论文,为了求得三体问题的通解,他用了一个非常特殊的例子作为问题的结果,即:如果某一时刻,三个运动物体恰恰处于等边三角形的三个顶点,那么给定初速度,它们将始终保持等边三角形队形运动。这个问题其实是有五个解的,分别是L1、L2、L3、L4、L5。

其实早起1767年,数学家欧拉根据旋转的二体引力场推算出其中三个点(特解)L1、L2、L3,1772年的时候拉格朗日算出另外两个点(特解)L4、L5。
拉格朗日点的首次证明是在1906年,天文学家沃尔夫发现了一颗行为怪异的小行星,它的绕日轨道与木星完全相同,在木星前方运行。看上去,小行星-木星-太阳,三者总是呈等边三角形,这颗小行星被命名为“阿基里斯”。

科学家很快意识到,这或许就是拉格朗日点存在的证据;很快,天文学家又在相反的的位置上,也发现了小行星,后来还发现了大量的小行星,存在于这两个点上,后来科学家将拉格朗日点运用到了地球上。
如图示,欧拉发现的点均在上图的X-轴上。M和M1,M2比质量过小而不影响M1和M2的运动轨迹。M1,M2可为地球和月亮(地月系统),也可为地球和太阳(日地系统),简单来说就是地日系统和地月系统都可以看作是限制性三体问题,因而涉及地球的拉格朗日点其实有两组。