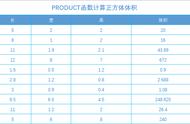
最后,还要将长方体体积与正方体体积公式统一成“底面积×高”,让学生理解长方体和正方体的体积公式之间的内在联系。结合长方体图形,说明计算公式中的“长×宽”就是它的底面积,则体积为“底面积×高”;再结合正方体图形,说明计算公式中的“棱长×棱长”就是它的底面积,而另一条棱长可以看作是正方体的高,则体积也是“底面积×高”。这样,就把二者的体积公式统一起来了,为后面学习圆柱体体积计算公式作了铺垫。

“圆柱的体积”是人教版数学六年级下册第三单元的学习内容。教材第24页直接提示学生“我们会计算长方体和正方体的体积,怎样计算圆柱的体积呢?能不能将圆柱转化成我们学过的立体图形,再计算出它的体积呢?”这里用到了转化的数学思想,即把新的问题转化为已学过的问题来解决。其实,在学习“圆的面积”时用过这种方法。当时是把圆形切成若干偶数份然后拼插成长方形来进行面积公式推导的。现在,得把这种方法迁移到体积公式的推导上。

同样的,借助教具演示把圆柱底面分成若干个相等的扇形,再拼插起来,得到一个近似的长方体。将拼成的长方体与原来的圆柱比较,发现长方体的底面积等于圆柱的底面积,长方体的高等于圆柱的高,从而推导出圆柱的体积公式也是“底面积×高”。

学习“圆锥的体积”时,教材第32页直接提出问题:“我们会计算圆柱的体积,怎样计算圆锥的体积呢?”通过圆柱、圆锥相互倒沙子或水的实验发现:等底、等高的圆锥和圆柱,圆锥的体积是圆柱体积的三分之一。由此得出圆锥体积的计算公式是“1/3×底面积×高”,即“v=1/3sh”。