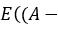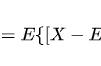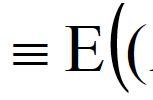其中 || x || 是向量 x 的大小(或「长度」)(参考勾股定理), 是箭头向量之间的角度。

正如一个 Python 函数:
def magnitude(x):
x_sq = [i ** 2 for i in x]
return math.sqrt(sum(x_sq))
我们通过将点积除以两个向量大小的乘积的方法得到 cos()。

def cosTheta(x,y):
mag_x = magnitude(x)
mag_y = magnitude(y)
return dotProduct(x,y) / (mag_x * mag_y)
现在,如果你对三角学有一定了解,你可能会记得,余弦函数产生一个在 1 和 -1 之间震荡的图形。

cos() 的值将根据两个箭头向量之间的角度而发生变化。
当角度为零时(即两个向量指向完全相同的方向),cos() 等于 1。
当角度为 -180°时(两个向量指向完全相反的方向),cos() 等于 -1。
当角度为 90°时(两个向量指向完全不相关的方向),cos() 等于 0。
这可能看起来很熟悉——一个介于 1 和 -1 之间的衡量标准似乎描述了两个向量之间的关系?那不是 Pearson’s r 吗?
那么——这正是它的解释!通过将数据视为高维空间中的箭头向量,我们可以用它们之间的角度 作为相似度的衡量。