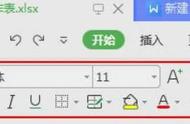
Photo taken at the Bourbaki founding congress in Besse-en-Chandesse, July 1935. Standing left to right: Henri Cartan, René de Possel, Jean Dieudonné, André Weil and Luc Olivier (a biologist). Seated left to right: a “guinea pig” named Mirles, Claude Chevalley and Szolem Mandelbrojt.
Grothendieck(格罗滕迪克)
20世纪60年代,Grothendieck领导的代数几何革命袭卷了整个数学界。
那时总有些人对他的理论表示很不理解。
一次Tate John做了一张小纸片,Grothendieck就把它放在他的上衣口袋里,每当有人提出议疑时,他就会把小卡片拿出来,上面写着:"there may be nilpotent elements in it”。
Grothendieck 1951年刚到法国Nancy时,写了一篇50多页 的文章给Dieudonne,题目是: ”Integration with values in a topological group” 内容很详尽,但是没有什么意思。 Dieudonne把Grothendieck教训了一顿,告诉他应该研究有意义的数学 问题,为了抽象而抽象是没有前途的。 后来Dieudonne 和Schwartz在一篇文章最后提出了14个未解决的问题, 并让Grothendieck去试试。 几天后,当Grothendieck再次出现在他们面前时,一半的问题已经被解决了。 从此,法国数学界开始对这个没有接受正规数学训练的小子刮目相看了。
曾在Princeton读书的几个学生给数学界的VIP写过一些打油诗,其中有一个是给Grothendieck写的,其中一段是:
His secretary Dieudonne,who does the writing up and such
Is gratefu for his patronage and thanks him very much
So my mind was filled with wonder when in the news I read
Alex Grothendieck gave up math—and took up politics instead
But I,I work on my PhD
And I curse the life I am living
And I curse my poverty
And I wish that I could be
Alex Grothendieck


Vietoris,Leopold
Vietoris,Leopold (1891--2002),可能是世界上最高寿的数学家了。
Vietoris是奥地利数学家,1920年在Wien大学获得博士学位,1930-1961在Innsbruck大学任教。Vietoris的主要数学贡献在代数拓扑领域,众所周知的Mayer-Vietoris序列,Mayer在1926/1927年向Vietoris学习代数拓扑。Hirzebruch在1996年9月曾写信问过Vietoris此事,连他都很犹豫给一个105岁的老人写信是不是合适,几周后,Hirzebruch居然收到了回信。
除了拓扑学外,Vietoris在概率方面也有工作,特别是在他103岁时还写过一篇三角级数的文章。
Cohen,Paul(1934-)
Cohen,Paul(1934-)是迄今唯一一个在数学基础方面获得Fields的数学家。而且其早年的工作在调和分析方面。1961年,cohen证明了连续统假设与集合论其它公理的独立性。 随后,他被邀请去法国做报告,法国所有的数学基础专家都去了,他是这样开场的:“过去30年来,没有人对这个问题做出突破性贡献,但这并不奇怪,因为自Godel以后,没有一流的数学家在这个领域内工作”。 Cohen在chicago大学读研究生时,有一次英国数学家Swinnerton-Dyer来访,Cohen对他说他在Landau的书里读到一个Siegel定理,现在正在考虑把这个定理改进到最优的结果 Swinnerton-Dyer很负责的说,这个东西呀,在我们有生之年是看不到解决的希望了。 过了几天,SD主动来找Cohen,说你前几天说的那个东西已经被我的同胞Roth,Klaus解决了,特来向你道歉。 过了几年,Roth因为这项工作被授于Fields奖。
Poincare(庞加莱)猜想引无数英雄竟折腰
在数学中,有一些表达十分简洁的命题却揭示了深刻的数学内涵 比如Goldbach猜想和Poincare猜想,正是因为如此他们都吸引 了大批的数学家去攻克这些问题,poincare猜想是低维拓扑中 的中心问题,Papakyriakopoulos,Christos一个在princeton 工作的希腊数学家,对低维拓扑有重要贡献,他去世后,人们发现 他的一个160页的手稿,是一个证明poincare猜想的大体计划,在其中一页的上面,有一个“引理14”可是没有给出证明。
1963年,一个德国数学家听从他的妻子(也是一个数学家)建议,去搞 poincare猜想,此前他做的是和钮结有关的问题,不过他的复杂的非 代数方法没有引起主流数学界的关注。经过10年不断的失败,他实在是 受不了了,改行做四色猜想的证明,不出几年就成功了。这个人就是 Haken,Wolfgang,有一类以他的名字命明的流形在poincare猜想的研究 中十分重要。
Conner,Andrew是Auburn university的一个 数学教授,一生痴迷于poincare猜想的证明, 在他1984年43岁因癌症去世前,他又宣布了他的 一个证明,并把Haken和另外四个数学家叫到病床 前检查他的证明,但是他此时已经不能和别人讨论 问题了。
Rourke,Colin是英国Warwick大学的数学教授, 1985年他的一个博士后Rego,Eduardo证明了一个 定理,Rourke马上发现这个定理可以推出poincare 猜想。1986年11月,他在UC Berkeley开了一个 讨论班讲他的证明,听众有Kirby,Gabai,Casson Rourke的一个学生Kazez,还有Kirby的两个研究生 Hirsch,Mike和Walker,Kevin 在最后一天,错误终于被发现了,这是Haken六个月前 指出的,很不幸,Rourke最终没有能干掉它。
Gabai,David
Gabai,David,2004年获得Veblen奖低维拓扑专家。 有人说如果Thurston说poincare猜想 被证明了,并把它写在一页纸上,大家会 争着去搞到他的手稿。 如果Gabai说poincare猜想被证明了,大家 肯定会相信他,但没有人会去读他的证明。
Springer-Verlag出版社
据统计,在数学类的各类出版物中,有一半以上 是Springer-Verlag出版的, 比如Lecture Notes in Mathematics, Graduate Texts in Mathematics。
Springer-Verlag是Julius Springer在1842年 开创的,最初只是一家书店,后来业务不断壮大, Julius Springer是一位国际象棋的爱好者, 从1881年开始,Springer-Verlag用象棋中的马 的图案作为其标志,因为Springer这个词在德文 中意即“象棋中的马”。
1906年,Ferdinand springer开始经营这个出版社,据说他本人是个生物遗传学家,并且是Springer-Verlag的一个期刊的编辑。在二战快结束时,他被俄军俘掳,审训官问他是个干什么的人,他回答说是个出版商,出版了 100多种杂志,并把刊名都写出来,当他写到90多个时,那个审训官说好吧,你可以走了,我在这个杂志上发表过文章!不过建议你还是跟着我们,以免再被不懂科学的人抓起来。
Hilbert(希尔伯特)
Hilbert晚年时有一次在家里举行一个宴会。
其间他的夫人发现他戴了一条脏领带,于是勒令他去换一条干静的,但是过了很久Hilbert也没有回来,夫人回去一看结果Hilbert已经躺在床上睡觉了。
按照Hilbert的逻辑,就是拖外套,解领带,拖衬衣,等等,然后睡觉。
Gleason,Andrew
Gleason,Andrew(1921-)是美国数学家,1986年国际数学家大会主席。
在Hilbert第五问题上有重要贡献,大概也是当今数学界唯一一个没有博士学位的人。
一般人很难和他与越南战争联系在一起。据说Gleason1940年在Harvard上大学时,有一个室友叫Bundy,McGeorge(1919-),原先打算去学数学,但是他发现Gleason也学了数学,怕是以后在数学界是没有出头之日了,所以就选择了政治,现在人们都知道,Bundy发动了越南战争。
陈省身和丘成桐下了一盘中国象棋。后来郑绍远问丘成桐结果如何?丘成桐声称自己赢了,后来丘成桐没有再和陈先生下过中国象棋。丘成桐的话也许是可信的,因为后来他赢了郑绍远以后,也不再和郑绍远下中国象棋了。
Abhyankar,Shreeram S
现在在Purdue University,研究代数几何中的奇点解消问题,是Zariski在Harvard的学生。
Abhyankar早年在University of Bombay与Birkhoff,Garrett学习代数,后来听了Zariski的一个关于射影几何的演讲决定去和Zariski学代数几何。
Zariski
Zariski对学生的要求十分严格。据说有人曾警告他说:“如果你永远不想毕业,那就去跟Zariski好了”。Zariski,Oscar20世纪60年代在哈佛大学建立了代数几何中的“哈佛学派”,据说他是唯一一位在活着的时候把半身像挂在哈佛大学数学教室里的人。Zariski很少收学生,有时既便收了,也马上推荐给其它教授。
下面是从1942年开始在Zariski门下获得博士学位的人:
Shreeram Abhyankar Harvard University 1956
Michael Artin Harvard University 1960
Irvin Cohen The Johns Hopkins University 1942
Peter Falb Harvard University 1961
Irwin Fischer Harvard University 1953
William Fishback Harvard University 1952
Daniel Gorenstein Harvard University 1950
Robin Hartshorne Princeton University 1963
Heisuke Hironaka Harvard University 1960
Steven Kleiman Harvard University 1965
Joseph Lipman Harvard University 1965
Harry Muhly The Johns Hopkins University 1940
David Mumford Harvard University 1961
Maxwell Rosenlicht Harvard University 1950
Abraham Seidenberg The Johns Hopkins University 1943
其中就有两位Fields奖得主,其中一位广中平佑(Hironaka)是Zariski在日本淘来的,1956年,Zariski访问日本,参加了秋月康夫(Akizuki,Yasuo)的一个讨论班,这个讨论班 的成员有永田雅宜(Nagata,Masayosi),松村英之(Matsumura,Hideyuki),户田宏(Toda,Hirosi),伊藤清(Ito,Kiyosi),井草准一(Igusa,Jun-Ichi)等人,后来都成了著名的数学家 广中平佑在上面做了一个报告,尽管他的英语表达让Zariski很不舒服,但是确出人意料的推荐广中去哈佛大学留学,广中后来回忆说:这对当 时的日本青年来说,was a case of Dream-Come-True。日本人好像是天生英语能力不行,广中平佑也不例外。刚到美国时,由于经济紧张,Zariski给他介绍了一个工作,让他去给大学研究生院的学生教课,每次给5美元,结果学生听不懂广中说的英语,上了两次就把他辞了。Zariski看他买书没有钱,就从自己的工资袋里拿出几张纸币借给他,后来据广中说他都还清了。
据说thom曾经说过做代数几何的都是废物点心,因为他们一遇到解决不了的问题就会说其实真要是解决了也没有什么意义。
奇点的解消就属于这种问题,有人说要解决它必须等到代数几何发展到一定程度,可是真要是达到那个程度,这个问题对代数几何也就没有什么意义了。
广中在思考这个问题时曾和Grothendieck讨论过,可是Grothendieck对这个问题没有兴趣。
广中在Brown university任教时,在有一次在harvard遇见Zariski,Zariski把他叫住问他最近在做什么,广中回答说他正在考虑一般的奇点解消问题,Zariski自己在低维的情形做过重要贡献,他想了一会说:“you need strong teeth to bite in!”。用广中自己的话说就是“勒紧裤腰带加油干!”。
在Brown university工作的第二年,广中平佑基本上就把一般的奇点解消问题解决了。消息公布以后,Zariski似乎还有些不太相信,有一次他问广中:is your resolution still a theorem?。
然后就开始写论文,通常是晚上十点开始写,写到第二天早晨五点钟上床睡觉,他的妻子广中和歌子不久起床后数一数写了几页,然后用打字机打印出来。一直这样写了两个月,终于完成了
论文发表在annals of mathematics上面。据说原稿有麻省的电话号码簿那么厚,所以以后数学界用“广中的电话簿”来指那篇文章。
后来广中回忆说:那段时间把精力都用在这个问题上,每天只睡三四个小时,结果是在学校上课只能是应付,上他课的学生算是倒霉了,呵呵
Erdos,Paul
Erdos,Paul据说是随时随地都能思考数学问题。他的大脑向每个人打开,下面是他在庆祝我国数学家柯召80寿辰时的一段话
I visited china twice.first in january 1960 i stayed for about three weeks.ko met me with hua at the airport.hua who is also one of my old friends is unfortunately no longer alive. in the summer of 1986 i was in JiNan at the chinese-American combinatorial meeting and spent a short time in Peking and had the good fortune to meet ko.his daughter and grandchild.I very much hope to meet ko soon again But enugh of the idle talk let 1<a1<a2....<ak<n be a sequence of integers ………………
柯召在英国Manchester大学的导师是Mordell,他给柯召的第一个题目是“关于Minkowski猜测”柯召专心思考了整整一周,结果毫无头绪后来Mordell对他说:“这个问题我搞了三年也没有解决”。
两个月后,柯召完成了一篇很有创见的论文,Mordell让他去伦敦数学会报告这篇文章,在这之前,还没有中国人登过伦敦数学会的讲台,Hardy当时也在座,对此印象极深,后来他在主持柯召的博士论文答辩时说:“你已经做过报告了!”。
Schwartz,Laurent
Schwartz,Laurent(1915-2002)在参加巴黎高师入学考试的口试时,听到考官问他前面的那个人一个问题,大意是为了有某个性质,两个数x,y要满足什么代数关系,那个人很快就答出来了,x,y关于一个一元二次方程的根是调和共轭的,并给出一个几何解法,因次他通过了考试。
后来Schwartz向那个人表示祝贺能想出这么巧妙的解法,“你知道,我已经是第三次做这道题了!”。
PS:过去欧洲的学生参加大学预科考试都有专门的“教授”指导,这些人一般不做学术研究,但要求精通考试训练。
Levy,Paul
Schwartz,Laurent的岳父是Levy,Paul(1886-1971),一个干瘪的法国老头,是Hadamard的学生,在概率和泛函分析方面工作,functional analysis这个词就是他最先引进的。
有一次Schwartz问他是否知道Lebesgue’s theorem of density的简单证明,“我见到过几个,但是现在都记不得了,不过我可以想一下找出一个证明”,半个小时以后,他给出了一个漂亮简洁的证明。6个月后,当Schwartz再次向他提到这个证明时,“啊!多么好的想法!我从未想到过这个”,当Schwartz告诉他这就是他6个月前发现的证明,Levy根本不相信。
Levy,paul这个人数学做的虽然不错,但是记忆力却很差。有一次Errera,Alfred(1886-1960)(Landau的一个学生)为Levy举办了一场晚宴,第二天,Errera碰见Levy,毕恭毕敬的说:“我很高兴昨天度过一个美好的夜晚”。“恩?那么你昨晚在哪?”。
Weil, Andre
Weil,Andre(1906-1998),一个不懂物理自以为数学很牛的法国人。
在一次数学系圣诞宴会上,坚持把自己列为有史以来最牛的十个数学家之一。
还有一次在Princeton的一次聚会上,一个研究生问每个人谁在20世纪数学家中排第一,当问到weil时,回答是Siegel,Ludwig(1896--1981),“那么谁是第二?”,weil笑了,然后指了指他自己...
有一天weil碰见Wiener,两个人都学了点中文,就用“中文”聊了半天,chern正好当时在场,就问旁边的一个学生“请问你能告诉我他们说的是哪国语言吗?”。
weil由于害怕打仗在1939年从法国去了芬兰。后来二战爆发了,苏联开始轰炸芬兰。有一天芬兰警方在weil的住所发现了一堆写满奇怪符号的手稿和一封苏联数学家Pontrjagin写给Weil的信,所以weil马上被当做间碟抓了起来。不过由于一次偶然的机会,被芬兰数学家Nevanlinna,Rolf Herman(1895-1980)营救了出来。后来在被送往法国的客船上,weil意外的在一次早餐餐厅里遇见了法国数学家Frechet,Maurice-Rene(1878-1973)一行人,Frechet悄悄跟weil说:“在London,人们都说你在芬兰被当作间碟抓起来了,不过我不相信,因为要是那样子你早就被干掉了!”。“His axiomatic reasoning was impeccable”后来weil得意的说。
weil在1940年初被送回法国,关在一个叫“Bonne-Nouvelle”的监狱里,几个月里在代数几何方面取得了重大突破。后来Cartan,Henri(1904-)写信给weil说:“并不是我们每一个人都能和你这么幸运能在这么安静的环境下工作”,还有一次weil在作报告时有个地方证明不下去了,weyl,Hermann(1885-1955)建议他再回监狱里呆几个月。尽管weil对做囚犯情有独衷,不过5月份当法庭让他在“5年监禁”和“在军队里服务”两者之中选一个时,他选择了后者。不过,这一次他做对了。几天后,因为德军的日益逼近,这个监狱里的犯人全部被处绝。
20世纪50年代,weil和Halmos,paul(1913-)同是Chicago大学的数学教授。有一次weil读到一篇揭露Bourbaki“骗局”的文章,马上署名Bourbaki写信给编辑部,企图说明说Bourbaki这个人是存在的,并说他最近被ASL(Association for Symbolic Lgic)邀请去作报告,还说可以让他Chicago大学数学系主任Mac Lane,Saunders(1909-2005)做证。
然后weil便气势凶凶的闯进Mac Lane的办公室,把这封信往桌子上一扔,然后说:“Saunders,如果你不告诉他们事实‘真相’,我以后就再也不跟你说话!”。Mac Lane 没有办法,只好迫于压力写了一封含糊其词的“证明信”。
至于Halmos,Mac Lane后来抱怨说,我们并没有给他加工资,可是那家伙仍赖在Chicago大学不走。
Bers,Lipman
Bers,Lipman(1914 - 1993)。在二战时有一次路过美国,美国政府马上把他的护照给扣下了。Bers提出强烈的抗议:“but how can i live without a passport?! i am naked i can‘t walk!”
据说官方的答复是:“you walk with your legs,not with a passport”。
Jean-Pierre Serre
Serre, Jean-Pierre(1926-)1954年28岁拿到Fields奖。虽然数学做的不错,但是也是那种很吊的数学家。Bott说serre是那种叫做“smart mathematician”的人。在公共场合你看到他看报纸,下棋,很少看到他在做数学,如果你问serre一个问题,他会马上告诉你答案,否则就是拒绝回答,后一种情况如果你再问他是否想过这个问题时,他会说如果不知道答案就没法思考!
据serre的夫人说serre常常是半夜起来做数学,而serre自己却说他最重要的数学发现都是在睡觉的时侯想出来的!
在数学界有一个众所周知的serre猜想,它是说:“域上的多项式环上有限生成投射模是否一定是自由的?”。这是serre在1955年FAC中提出来的,其实它最早是Grothendieck在给serre的一封信里出现的。后来Grothendieck在讨论班上提出了Riemann-Roch定理的一个一般的证明,也没有最后发表,而是由serre和Borel整理发表在Bull.Soc.Math.France上面。
Grothendieck和serre都是当代法国的数学名家,两个人的风格可以说是迥然不同。 Grothendieck的思维方式是天马行空般从一个领域到另外一个领域,大刀阔斧的开创出新的数学领域而不注重细节。 serre的风格比Grothendieck细腻的多,他的脑子里有许多具体的问题。 有一次讨论班上,Grothendieck写了几黑板的数学问题,serre则只管看他带来的预印本,最后Grothendieck问是否可以把这些问题推广? serre于是放下预印本想了一会,然后举出一个反例。
有趣的是虽然Grothendieck和serre在1955年就开始通信讨论问题,但他们从来就没有一起发表过文章。
在这个世界上可能没有人比serre对具体问题和抽象推广的关系把握的更好的了.
serre的一个学生曾经回忆说在他做serre的PhD时,每当他遇到研究中的困难时,就会和serre在巴黎的一个小茶馆里约会,serre通常会比预定的时间早一点到达,然后要他把问题表述一遍,serre听完后会给出几个例子来说明他的学生的这种表达方式并不能得到好结果,并提出自己的见解.
很多人说serre的行文风格非常清晰.据说有一次serre在讲课的时侯描述了一个环,这时有个听众问他这个是不是chow环,回答是“I mean the ring studied by Chow and Samuel”。