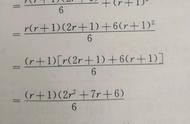分析:
显然,左式用常规求和方法是非常困难的,但是因为n的可以无限大,该等式也没有办法依次进行验证。
那我们不妨考虑,是否能用多米诺骨牌的原理去进行说明?
比如:首先验证n=1时,等式成立;
再验证如果n=k等式成立时,看能否证明n=k 1时等式也成立。如果也成立的话,那是不是就有点多米诺骨牌的意思了呢?
证明:



综合(1)(2)可知,
原等式成立。
这种方法称之为“数学归纳法”。
其中,第一步为“归纳基础”,
相当于“第一块骨牌成功倒下”;
第二步为“归纳递推”,
相当于“前一块骨牌倒下,引起了后一块骨牌的倒下”。
有了这两个条件,对于所有的n来说,等式都是成立的(相当于所有的骨牌都能倒下)。
数学归纳法
数学归纳法的基本原理