我们运用这个原则,以自然循环数列为例,按照文章最开头的机器约束矩阵和加工时间矩阵,作一个甘特图,说明这个数列实际上可以表示工厂作业排序优化问题的解。

这里小智要解释一下,这个甘特图表示了工厂生产玩具的工作流程。图中每一个方块表示一个任务,方块当中标志的数字是指玩具的编号。这个甘特图,横坐标表示时间轴,纵坐标表示机器。从这个甘特图可以发现,一共有M1-M6,六台机器。
最后可以发现,按照这个工作顺序生产玩具,一共生产时间为64分钟。
此时小智重点观察自然循环序列前两位:12,按照这个顺序来执行加工任务,以甘特图来印证:
Step1:执行玩具1的工序1,由机器2来执行,时间为10分钟,对应甘特图机器坐标为M2,时间坐标为0-10。
Step2:执行玩具2的工序1,由机器5来执行,时间为3分钟,对应甘特图机器坐标为M5,时间坐标为0-3。
第3-6步基本类似。我们再聚焦自然循环列第7-10位:1234。按照这个顺序继续执行加工任务, 以甘特图来印证:
Step7:执行玩具1的工序2,由机器3来执行,时间为9分钟。玩具1工序1的结束时间为10,而且机器3先前没有其他任务安排,所以玩具1工序2任务的甘特图机器坐标为M3,时间坐标为10-19。
Step8:执行玩具2的工序2,由机器1来执行,时间为6分钟。玩具2工序1的结束时间为3,而且机器1先前没有其他任务安排,所以玩具2工序2任务的甘特图机器坐标为M1,时间坐标为3-9。
Step 9:执行玩具3的工序2,由机器5来执行,时间为9分钟。玩具3工序1的结束时间为5,机器5先前有任务安排,加工的最后时间为8,所以玩具3工序2的开始时间为 max(5, 8) = 8,甘特图机器坐标为M5,时间坐标为8-17。
Step10:执行玩具4的工序2,由机器1来执行,时间为7分钟。玩具3工序1的结束时间为14,机器1先前有任务安排,加工的最后时间为9,所以玩具4工序2的开始时间为 max(14, 9) = 14,甘特图机器坐标为M1,时间坐标为14-21。
……
流程走到这里,相信大家对整个过程比较明朗了。
按照这个过程,自然循环序列就转变为一张甘特图,进而可以计算出整体的完成时间。
进一步地而言,任何自然循环序列打乱以后的序列,都可以表示这个工厂作业生产优化问题的解。
此时,我们就应该明白解的构造方式了。那接下来这道问题中另一关键点,那就是老解如何变换才能产生新解。
由于目前解的构造方式是一组编码,因此可以对这组编码进行重排,即可产生新解,但也需要考虑到保留当前解的有效成分。
考虑以最简单的方式来产生新解,随机调换:在当前解中随机选择两个位置,并对调它们的数值。

更换第6个位置和第26个位置的数,产生新解

算法思想、解的构造、解的产生,这三大问题终于解决了,小智开始设计模拟退火的实现过程了:
第1步,初始化,取一个足够大的初始温度 T0,令当前温度 T = T0,给定一个初始解S1。
第2步,随机调换当前解 S1 的两个位置的数值,产生一个新解 S2 。
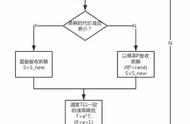
第3步,计算增量,Δ = f(S2)– f(S1),其中f为计算解的总生产时间的函数。
第4步,如果 Δ < 0 则接受 S2 作为新的当前解,S2 = S1 。否则,计算 S2 的接受概率