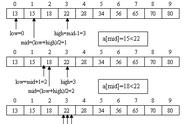
这段代码非常短,只有两重循环,结合之前的描述应该很容易理解。我们复杂度分析也很简单,从两重循环入手的话,我们显然是 O(n^2) 。我们也可以从状态数和决策数入手,我们每一个结尾的答案是状态,数量是n。对于每一个状态而言,它有可能跟在面面的每一个位置后面,所以潜在的决策数最坏也是n,所以整体的复杂度是 O(n^2) 。
虽然我们花费了很多笔墨,但是这个算法并不困难,的确是高中生竞赛的难度。但别着急,问题还没有结束,我们的下一个问题是,这个算法还有改进的空间吗?
进阶
既然这个问题问出来,显然答案是确定的。如果你在面试当中被面试官问还能有优化吗,你要是答没有,那可是会扣很多分的。面试官不是觉得你太鲁莽了就是觉得你情商捉鸡,所以如果面试的时候被问题,一定要回答有,至于怎么优化,那可以慢慢想,答不对都没问题,要是基调就定错了,可是很严重的。
动态规划问题的优化其实只有两种情况,要么从状态数入手,减少多余的状态数,要么从决策入手,快速找出正确的决策。比如之前介绍的单调优化就是后者,一般情况下来说状态数都是比较固定的,也是很难减少的,往往优化都要从决策上入手。这题也不例外,那么我们怎么来优化呢?
想要优化,眼前的信息是不够的,算法都不是凭空想出来的,往往是推导出来的。我们还需要更多的信息和结论才行,对于每一个要求的i 1位置而言,我们已经知道了它前面所有答案的情况。如果我们可以设计一个方法,快速地找到i 1究竟应该跟在哪个位置后面就好了。
这个方法我们干想是想不到的,必须要结合数据。我们用上面的样例来举例,画出所有位置最佳的转移决策:

好像也看不出什么眉目来,我们随意挑出一个元素来仔细查看,假设我们就挑选207。我们列举出207之前所有的位置的元素和答案,并且按照元素大小进行排序,可以得到这样的结果:

其中的155和158的长度都是2,显然我们可以去除掉158,只保留155。因为155 < 158,155能转移到的位置158一定也可以。我们把这个结论推广,也就是说对于长度相同的位置,我们只需要保留其中最小的那个。
我们观察上面这个序列,好像数字越大的长度也就越大,长度越大的数字也就越大,但真的是这样吗?我们试着更改一个值:

我们把158改成358,好像就不满足了,虽然358很大,但是它的答案很小。但是当我们根据上面的原则去重之后,我们剩下的序列还是递增的。这个只是巧合还是的确如此呢?
我们可以试着证明一下,假设存在反例。我们假设数组当中存在两个数x和y,这两个数同时存在于去重之后的答案数组当中。其中x < y,并且x的答案大于y。根据我们刚才排序的逻辑,那么x应该排在y的左侧。数组当中比x小的那些值必然也出现在x的左侧,那么必然存在一个位置的答案和y相等并且数值小于y,那么y必然会被去除,所以就和x和y同时存在矛盾了。
我们用下图来展示一下上面列举的反例。