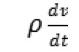这里的μ(n)叫做莫比乌斯函数(Möbius function)。没错,就是莫比乌斯带的那个莫比乌斯(August Ferdinand Möbius,1790 - 1868),这又是一位伟大的德国数学家。

莫比乌斯带
莫比乌斯函数的取值只有三种可能:0和正负1。如果n可以被任何一个质数的平方整除,也就是说在它的质因数分解中有一个质因数出现了二次或更高次方,那么μ(n) = 0。如果n不能被任何一个质数的平方整除,也就是说n的任何一个质因数都只出现一次,那么我们来数质因数的个数。假如质因数有偶数个,那么μ(n) = 1。在这里还包括了n = 1的情况,因为它没有质因数,0算作偶数,所以μ(1) = 1。而假如质因数有奇数个,那么μ(n) = -1。
由此可见,μ(1) = 1,μ(2) = -1,μ(3)= -1,μ(4) = 0,μ(5) = -1,μ(6) = 1等等。这正是上面的展开式中用到的前几项。
很显然,J(x)是一个增函数。在上面的展开式中,随着n的增加,x的1/n次方变得越来越小,相应的第n项也变得越来越小。因此,对π(x)贡献最大的就是第一项,J(x)。而对J(x)贡献最大的来自哪一项呢?这就涉及到黎曼ζ函数非平凡零点的位置了。
一个非平凡零点ρ的实部和虚部经常被记为σ和t,即ρ = σ it。黎曼很快就证明了,ρ不可能出现在σ > 1或者σ < 0的地方。也就是说,非平凡零点只可能出现在0 ≤ σ ≤ 1的区域里。在复平面上,这对应于一条宽度为1的竖直条带,人们把它称为临界带(critical strip)。
然后,根据黎曼ζ函数的形式,很容易发现零点对于实轴是对称的。也就是说,如果σ it是一个零点,那么它的共轭复数σ - it也是一个零点。因此,非平凡零点总是上下成对出现的。当我们说第n个非平凡零点的时候,指的总是第n个虚部为正数的非平凡零点,而虚部为负数的那些自动地就知道了。
再然后,根据黎曼的函数方程,即ζ(s)与ζ(1 – s)之间的联系,又很容易发现,非平凡零点对于σ = 1/2这条竖线是对称的。也就是说,如果σ it是一个零点,那么1 - σ it也是一个零点。
黎曼计算了几个非平凡零点的位置,发现它们的实部都等于1/2。例如第一、二、三个非平凡零点,实部都等于1/2,而虚部分别约等于14.1347、21.0220和25.0109。然后,他就做出了一个惊天动地的猜想:
黎曼ζ函数所有的非平凡零点,实部都等于1/2!
这就是黎曼猜想,数学中最大的未解之谜之一。
我们把σ = 1/2的这条竖线称为临界线(critical line),也就是临界带的中心线。前面我们已经知道了,所有的非平凡零点都在临界带里。但黎曼猜想却大大地加强了这个结论,它说的是:所有的非平凡零点都在临界线上!

临界线与临界带
这是一个非常令人惊讶的结论。假如非平凡零点的实部是在0到1之间随机取值,那么它刚好取到1/2的概率应该等于0。而现在黎曼却认为这个概率是100%!这件事如果是真的,就说明它一点都不随机,在这背后肯定有深刻的原因。
黎曼猜想到底对不对呢?目前还没有被普遍接受的证明或证伪。但数值计算的结果,已经为这个猜想提供了强有力的支持。
到目前为止,人们已经计算了十万亿个非平凡零点。然后你猜怎么着?这十万亿个非平凡零点都整齐划一地躺在临界线上。十万亿!因此,绝大多数数学家都相信黎曼猜想是正确的。
黎曼猜想有什么用呢?我们可以举一个容易理解、也意义重大的例子,这是一个在探索黎曼猜想的过程中得到的中间结果。
来问你一个问题:在1到10的100次方的范围内,大约有多少个质数?
数学王子高斯小时候就研究过质数分布的问题。怎么研究呢?每当他有空的时候,就挑出几个长度为1000的自然数区间,算出这些区间中的质数个数。你看,这就是高斯的消遣!

高斯
显然,随着数字的增大,质数一般而言会变得越来越稀疏。但具体是怎么个稀疏法呢?在做了大量的计算和比较之后,高斯发现质数分布的密度大约是对数函数的倒数,也就是说,在x附近的一个数是质数的概率大约是1/lnx。你看,数学家的消遣能够结出什么样的果实!后来,法国数学家勒让德(Adrien-Marie Legendre,1752 - 1833)也得到了同样的结果。