3.问题探究:
(一)新知学习:
圆内接四边形的判断定理:如果四边形对角互补,那么这个四边形内接于圆(即如果四边形EFGH的对角互补,那么四边形EFGH的四个顶点E、F、G、H都在同个圆上).
(二)问题解决:
已知⊙O的半径为2,AB,CD是⊙O的直径.P是弧BC上任意一点,过点P分别作AB,CD的垂线,垂足分别为N,M.
(1)若直径AB⊥CD,对于弧BC上任意一点P(不与B、C重合) (如图一),证明四边形PMON内接于圆,并求此圆直径的长;
(2)若直径AB⊥CD,在点P(不与B、C重合)从B运动到C的过程中,证明MN的长为定值,并求其定值;
(3)若直径AB与CD相交成120°角.
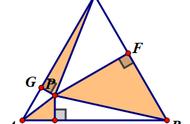
①当点P运动到弧BC的中点P1时(如图二),求MN的长;
②当点P(不与B、C重合)从B运动到C的过程中(如图三),证明MN的长为定值.
(4)试问当直径AB与CD相交成多少度角时,MN的长取最大值,并写出其最大值.

【解析】:(1)如图一,
∵PM⊥OC,PN⊥OB,∴∠PMO=∠PNO=90°,
∴∠PMO ∠PNO=180°,
∴四边形PMON内接于圆,直径OP=2;
(2)如图一,∵AB⊥OC,即∠BOC=90°,
∴∠BOC=∠PMO=∠PNO=90°,
∴四边形PMON是矩形,∴MN=OP=2,
∴MN的长为定值,该定值为2;
(3)①如图二,∵P1是弧BC的中点,∠BOC=120°
∴∠COP1=∠BOP1=60°,∠MP1N=60°.
∵P1M⊥OC,P1N⊥OB,∴P1M=P1N,
∴△P1MN是等边三角形,∴MN=P1M.
∵P1M=OP1•sin∠MOP1=2×sin60°=√3,∴MN=√3;
②设四边形PMON的外接圆为⊙O′,连接NO′并延长,
交⊙O′于点Q,连接QM,如图三,

则有∠QMN=90°,∠MQN=∠MPN=60°,
在Rt△QMN中,sin∠MQN=MN/QN,
∴MN=QN•sin∠MQN,
∴MN=OP•sin∠MQN=2×sin60°=2×√3/2=√3,
∴MN是定值.
(4)由(3)②得MN=OP•sin∠MQN=2sin∠MQN.
当直径AB与CD相交成90°角时,∠MQN=180°﹣90°=90°,MN取得最大值2.