4.阅读理解:
如果同一平面内的四个点在同一个圆上,则称这四个点共圆,一般简称为"四点共圆".证明"四点共圆"判定定理有:1、若线段同侧两点到线段两端点连线夹角相等,那么这两点和线段两端点四点共圆;2、若平面上四点连成的四边形对角互补,那么这四点共圆.例:如图1,若∠ADB=∠ACB,则A,B,C,D四点共圆;或若∠ADC ∠ABC=180°,则A,B,C,D四点共圆.

(1)如图1,已知∠ADB=∠ACB=60°,∠BAD=65°,则∠ACD=______;
(2)如图2,若D为等腰Rt△ABC的边BC上一点,且DE⊥AD,BE⊥AB,AD=2,求AE的长;
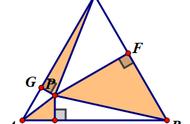
(3)如图3,正方形ABCD的边长为4,等边△EFG内接于此正方形,且E,F,G分别在边AB,AD,BC上,若AE=3,求EF的长.
【解析】:(1)∵∠ADB=∠ACB=60°,∴A,B,C,D四点共圆,
∴∠ACD=∠ABD=180°﹣∠ADB﹣∠BAD=180°﹣60°﹣65°=55°,
故答案为:55°;
(2)在线段CA取一点F,使得CF=CD,如图2所示:

∵∠C=90°,CF=CD,AC=CB,
∴AF=DB,∠CFD=∠CDF=45°,∴∠AFD=135°,
∵BE⊥AB,∠ABC=45°,∴∠ABE=90°,∠DBE=135°,∴∠AFD=∠DBE,
∵AD⊥DE,∴∠ADE=90°,
∵∠FAD ∠ADC=90°,∠ADC ∠BDE=90°,
∴∠FAD=∠BDE,
在△ADF和△DEB中,∠FAD=∠BDE,AF=BD, ∠AFD=∠DBE,
∴△ADF≌△DEB(ASA),∴AD=DE,
∵∠ADE=90°,∴△ADE是等腰直角三角形,
∴AE=√2AD=2√2;
(3)作EK⊥FG于K,则K是FG的中点,连接AK,BK,如图3所示:

∴∠EKG=∠EBG=∠EKF=∠EAF=90°,
∴E、K、G、B和E、K、F、A分别四点共圆,
∴∠KBE=∠EGK=60°,∠EAK=∠EFK=60°,
∴△ABK是等边三角形,
∴AB=AK=KB=4,作KM⊥AB,则M为AB的中点,
∴KM=AK•sin60°=2√3,
∵AE=3,AM=1/2AB=2,∴ME=3﹣2=1,