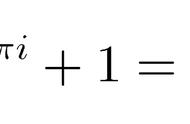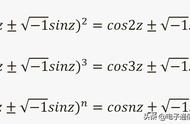e^iπ 1=0,这个高中生都看得懂的公式,很短,容易让人忽略它的高大上。
这就是欧拉公式,是瑞士天才数学家莱昂哈德·欧拉在1740年发现的。这个公式不仅隐含着深刻的数学思想,而且我觉得其中似乎隐藏着宇宙的真理。那么这个公式到底有什么魅力呢?

(一)数学中有五个最基本的常数:e、i、π、1、0,此公式居然用一个简洁的等式把它们非常优美的地串了起来。
①e被称为自然对数。e是无限不循环小数。收敛函数limn→∞(1 1/n)^n在n趋近于无穷大时,其值居然等于e.它能使复杂的运算变得简单。
②π:小学生都知道的圆周率,是圆周长和直径的比值。圆周长和直径的比值是居然是固定值,这个固定值居然是无限不循环小数,为什么圆形中包含着无限呢?难道圆周率就是宇宙?
③i:虚数单位。i²=-1,虚数其实就是负数的平方根。数轴只能表示实数,而复平面能表示所有数,复平面上的每两个点做任何运算,结果都对应复平面上的另一个点。复平面的神奇造就了i的神奇。
④1:1代表元首,代表开始,代表万物,堪称数字国王。1能被所有自然数除尽,却除不尽所有自然数。
⑤0:代表终点。宇宙始于0也终于0,黑洞的密度是除以0,无线能量的密度也是除以0,好深奥。
(二)其它符号:乘法代表结合,指数代表加成,加法代表累计,等号代表统一。
(三)证明过程也有奇妙之处。

(四)广义的欧拉公式e^ix=cosx isinx,随着x的增长,其数学图形绕着原点旋转,定义域在[-1,1]中往复,或许暗示了宇宙的无限膨胀和收缩。
欧拉公式暗示着:大自然是无限和有限的结合,最终归于终点0。
简洁又美丽的公式,或许只有爱因斯坦的质能方程能与之相媲美。
,