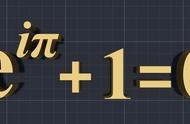他大火之后整理出来的小部分成果共包括886本书籍和论文,其中分析、代数、数论占40%,几何占18%,物理和力学占28%,天文学占11%,弹道学、航海学、建筑学等占3%,彼得堡科学院为了整理他的著作,足足忙碌了四十七年。
以欧拉命名的公式与定理,足足有数十个。这其中最为知名的就是我们的主体“欧拉公式”,这条恒等式第一次出现于1748年欧拉在洛桑出版的书Introduction,它是复分析的欧拉公式特例。。
欧拉公式并没有多复杂,反而方程简单,有点像武林高手,达到了最高境界,返璞归真一样的感觉。

看起来是不是特别地简单,但是这个公式在以前即使是许多的数学界穷尽一生都很难琢磨明白, 它将数学里最重要的几个常数联系到了一起:两个超越数:自然对数的底e,圆周率π;两个单位:虚数单位i和自然数的单位1,以及数学里常见的0。
那么为什么说这个公式非常复杂呢?因为你可以用非常多不同的方式去证明它,你既可以用数学归纳法证明,也可以用推理证明,也可以分式推导,还可以用复变函数求证,甚至你可以用 平面几何学、 物理学、拓扑学来推证。所以才说他蕴含了所有的数学元素,甚至蕴含了宇宙的至理法则。

自然数也被称为欧拉数的“e”含于其中。 自然对数的底、 素数定理、完全率、阻力落体、粒子运动,大到飞船的速度,小至蜗牛的螺线,都蕴含着“e"
而另外一个超越数,π,大家相比很清楚了,就是圆周率。这两个超越数都是欧拉发明的。
也包含了最重要的运算符号 ,最重要的关系符号 = 。而0和1,是构造群,环,域的基本元素,也是构造代数的基础。 而虚单位 i 使数轴上的问题扩展到了平面,在哈密尔的 4 元数与 凯莱的 8 元数中也离开不了它。
所以你明白为什么这个公式非常之复杂了吗?也正是因为其涵盖范围如此广泛,如三角函数、傅里叶级数、泰勒级数、概率论、群论等受到了它的影响。它同样对物理学影响也非常巨大,如机械波论、电磁学、波动光学以及引发了电子学革命的量子力学的理论基础也蕴含其中。 也将物理学中的圆周运动、简谐振动、机械波、电磁波、概率波等联系在了一起......
举一个例子,你可以使用欧拉公式将三角函数转换为指数(由泰勒级数易得):
sinx=[e^(ix)-e^(-ix)]/(2i) cosx=[e^(ix) e^(-ix)]/2 tanx=[e^(ix)-e^(-ix)]/[ie^(ix) ie^(-ix)]
cosα=1/2[e^(iα) e^(-iα)]sinα=-i/2[e^(iα)-e^(-iα)]
泰勒展开有无穷级数,e^z=exp(z)=1+z/1!+z^2/2!+z^3/3!+z^4/4!+…+z^n/n!+… 此时三角函数定义域已推广至整个复数集。可以说欧拉公式将指数函数的定义域扩大到了复数域,建立了三角函数和指数函数的关系,被誉为“数学中的天桥”。
还可以把它扩展为时间的函数。(引用至CSDN xieyan0811 )

加入了t,把e^(ix)想成e^(iwt),t是时间,w是系数。把平面上的转圈扩展成了空间中的转圈,纵轴表示时间t,两个横轴分别为实部(cos(t))和虚部(sin(t)),蓝线经过的点是e^ix,即,把时域上的e^ix分别投射到了实轴cos(t)和虚轴sin(t),它们都是时间t的函数.图中可看到正余和余弦的投射(红/绿)。如果用python做3D图,拖动旋转角度效果更直观.这就是傅立叶变换原理:将时域值拆分映射到频域,通过三角函数的叠加表示。
还有拓扑学里的欧拉公式
v f-e=x(p),v是多面体p的顶点个数,f是多面体p的面数,e是多面体p的棱的条数,x(p)是多面体p的欧拉示性数。 如果p可以同胚于一个球面(可以通俗地理解为能吹胀而绷在一个球面上),那么x(p)=2,如果p同胚于一个接有h个环柄的球面,那么x(p)=2-2h。 x(p)叫做p的欧拉示性数,是拓扑不变量,就是无论再怎么经过拓扑变形也不会改变的量,是拓扑学研究的范围。