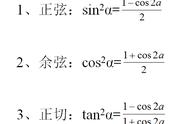在上篇文章()中,我们了解到了和函数的本质,它们的本质在于反映了沿圆心在原点的单位圆周上运动时横纵坐标的变化。
在本篇文章里,我们再推导一些基本的三角函数公式,包括和差公式、和差化积公式、积化和差公式。
首先我们需要推导三角函数和公式,也就是和。
C点在单位圆中沿x轴逆时针旋转角度得到B点,再继续旋转角度得到A点,如下图所示。并分别作于N点,于P点,于M,AP、OB相交与Q点。

单位圆
不难得出,B点坐标为,A点坐标为,于是,,,,,另外,。
到这里,我们也就推导出来了三角函数和公式:
现在我们再推导三角函数差公式,也就是和。
C点在单位圆中沿x轴逆时针旋转角度得到A点,再顺时针旋转角度得到B点,如下图所示。并分别作于N点,于P点,于M,AP、OB相交与Q点。

单位圆
不难得出,A点坐标为,B点坐标为,并且,,,,,另外,。
化简一下就可以得到:(1)
化简一下可以得到:(2)
联立(1)式、(2)式,就可以解出:
这里需要注意,当我们遇到难以化简的三角函数时,应该首先考虑利用来构造可以化简的项。
到这里,我们也就推导出来了三角函数差公式:
我们再以三角函数的和差公式为基础来推导和差化积公式。
需要注意,这里使用到一种常见的构造方法,即,。
基于上面几个式子,我们就可以推导出三角函数的和差化积公式:
最后,我们再基于三角函数的和差公式来推导积化和差公式。简单来说,就是将和差公式的左右对调,然后消去不必要的项。
欢迎关注、转发、收藏!
,