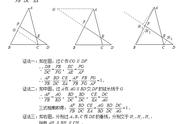
梅涅劳斯定理图解,梅涅劳斯定理的证明过程

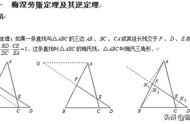
梅涅劳斯定理

一条直线经过三角形ABC的三个边，与AB， BC， AC分别交于H，

G, F , 证明：AH/BH·BG/CG·CF/AF=1

证明：从A， B， C分别做直线的垂线，

根据上面图形有多对三角形相似：

有比例：

将上述相乘即证得：

上述定理的逆定理也是成立的，即若H，G， F满足上述等式，那么这三点共线。

证明方法类似，可考虑HG直线与AC交于F’, 读者可自行证明F点与F’点是重合的。