cad计算扇形面积,cad计算弧形面积方法

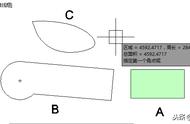
∵A（﹣2，0），B（2，0），

∴PA^²＝（m 2）^² n^²＝2^²①，

PB^²＝（m﹣2）^² n^²，AB^²＝16，

由PA^² PB^²＝AB^²得4 （m﹣2）^² n^²＝16 ②

由①②得到：m＝﹣1，n＝±√3，

∴P（﹣1，√3）或（﹣1，﹣√3）．

故答案为（﹣2，2）或（﹣2，﹣2）或（﹣1，√3）或（﹣1，﹣√3）．

（2）如图2中，∵PM⊥AB，∴∠AMP＝∠BMP＝90°，

在Rt△APM中，∵∠PMA＝90°，PA＝2，AM＝1，

∴PA^² PB^²＝4 12＝16，

∵AB^²＝16，∴PA^² PB^²＝AB^²，∴∠APB＝90°，∴△PAB是直角三角形．

（3）如图3中，连接EM．

∵PA^²＝4，AM•AB＝4，∴PA^²＝AM•AB，∴PA/AM=AB/PA，

∵∠PAM＝∠BAP，∴△PAM∽△BAP，∴PM/PB=PA/AB=1/2，

∴PM＝1/2PB，∴PE 1/2PB＝PE PM，

∵PE PM≥EM，∴PE PM的最小值为线段EM的长，

∵E（0，3），∴OE＝3，

【点评】本题属于属于圆综合题，考查了勾股定理以及逆定理，相似三角形的判定和性质，三角形的三边关系等知识，解题的关键是学会利用分类讨论的思想思考问题，学会构造相似三角形解决问题，学会用转化的思想思考问题，属于中考压轴题．

类型3 自定义问题

例3（2018•南通模拟）如图，⊙O的直径AB＝26，P是AB上（不与点A、B重合）的任一点，点C、D为⊙O上的两点，若∠APD＝∠BPC，则称∠CPD为直径AB的“回旋角”．

（1）若∠BPC＝∠DPC＝60°，则∠CPD是直径AB的“回旋角”吗？并说明理由；

（2）若弧CD的长为13π/4，求“回旋角”∠CPD的度数；

（3）若直径AB的“回旋角”为120°，且△PCD的周长为24 13√3，直接写出AP的长．