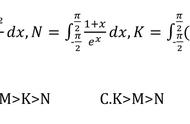作者 | 林开亮
来源 | 本文原载于《数学通报》,2022年第61卷第七期,p.54—60,感谢《数学通报》授权转载!本次转载,略有修订。
等幂差公式:一个主旋律的十一个变奏曲
1 序曲
首先声明,我不懂音乐。我对主旋律 (theme) 这个概念印象深刻,源于两篇科学史的通俗报告。一篇是法国数学家 André Weil (1906–1998) 的《数论今昔两讲》[19],另一篇是杨振宁先生的《量子化、对称和相位因子:20 世纪物理学的主旋律》[27]。至于变奏曲 (variation) 的观念,则是从一些数学书名注意到的,如 Victor W. Guillemin 和 Shlomo Sternberg 的 Variations on a Theme by Kepler(AMS,1990),Takashi Ono 的 Variations on a Theme of Euler:Quadratic Forms, Elliptic Curves, and Hopf Maps (Springer, 1994)。
最近,我了解到主旋律和变奏曲的观念其实早已渗透到数学教学中。例如,早在 40 年前,Abe Shenitzer (1921–2022) 在《数学教学》一文中就指出 [18, p. 112 ]:
如果我们同意强调特殊与普遍之间的互动是有效教学的一个重要元素,那么鉴于教学之实际,也许这样说是公允的:在数学教育的初级阶段,我们倾向于教变奏曲而不教主旋律;而在数学教育的高级阶段,我们倾向于教主旋律而不教变奏曲。
关于主旋律及其变奏曲,Shenitzer 举的一个典型例子,是 Gauss 的同余 (congruence) 概念。这个概念首先出现在高斯 1801 年出版的名著《数论研究》中:两个整数 称为模正整数 同余,如果 是 的整数倍(通常记作 )。对给定的正整数 ,按照模 同余关系,可将全体整数分成模 的同余类。例如,对 ,就得到两个等价类,分别是偶数类(模 2 同余于 0)与奇数类(模 2 同余于 1)。Shenitzer 指出,数学中的种种等价关系(我们从 C. Eckes 最近的文章 [5] 得知,等价关系的精确定义是由 Hermann Weyl 在 1910 年给出的。),都可以视为同余概念的变奏,如群作用下两个子集的等价、欧氏平面中两个图形的全等与相似,等等。在上述引文之后,Shenitzer 进一步问道:
你能给出其它数学主旋律及其变奏曲的例子吗?
对此开放问题,在中小学数学的范围内,一个极其值得注意的回答,已经由加州伯克利大学的伍鸿熙教授给出。他在写给小学、初中和高中的数学教师的一套师资培训教材 [20, 21, 22, 23, 24, 25] 中,曾多次提及这个极重要的主旋律——带余除法。
伍鸿熙教授在《数学家讲解小学数学》[20] 第四部分初等数论的引言中写道:“事实上,本书的第四部分或许可以视为对带余除法中余数的重要性的一个反思。”他在《有理数到线性方程》[23] 第三章欧几里德算法开篇写道:“本章本质上是带余除法的一组变奏曲, 其中主要的变奏是欧几里德算法。”
实际上,带余除法这个主旋律从小学、中学一直贯穿到大学,例如我们在高等代数中所学习的将整数(或多项式)矩阵化成 Smith 标准型,本质上就是求两个整数的最大公因子的扩充欧几里德算法的矩阵版本。坊间流传的“龙生龙,凤生凤,华罗庚的学生会打洞”,正是说华罗庚擅长用带余除法做初等变换将整数(或多项式)矩阵化成标准型。关于带余除法这个主旋律及其变奏曲,可以分享的非常之多,像欧几里德算法、中国剩余定理、线性丢番图方程组就是其中的代表。但我们今天不拟展开。
我们这里要分享的,是另一个主旋律及其变奏曲。某种意义上,它比带余除法更简单,但似乎没有引起足够的重视。
2 主旋律
本文将展开的主旋律,是一个极其简单的代数公式,如下:
设 是数, 是正整数,则有
(向左滑动查看完整公式,下同)
在 的特殊情况,(1) 就是平方差和立方差公式:
因此,我们的主旋律 (1) 不过是平方差公式 (2) 和立方差公式 (3) 的推广,也许可以称作等幂差公式。可以想见,正如 (2),(3) 可以直接证明那样,(1) 也可以如法炮制。这个简单的证明,我们留作练习。(1) 应当视为初中代数里的一个基本结果,正如伍鸿熙教授在《代数》[22]1.3 节为它所取的标题“A basic identity”所表明的那样。印度数学天才 Ramanujan (1887–1920) 的数学启蒙书《纯数学基本结果概要》之开篇([4, p. 33]),就是这个公式, 参见 R. Kanigel 所著《知无涯者:拉马努金传》[9]。
3 变奏曲
遵循伍鸿熙老师的思路,我们先介绍他在《代数》中所给出的等幂差公式 (1) 的两个变奏曲:梅森素数和有限几何级数。
3.1 梅森素数
当等幂差公式 (1) 中的 都取正整数且 时,容易看到,对一切 , 都是合数。例如,对 ,我们有
这就表明 是合数。
通常我们对素数更感兴趣。对 (1) 所给出的数,这就要求 ,在最特殊的情况 ,此时 (1) 所给出的数形如 。我们来看一些例子:
| n | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 | 8192 | 16384 | 32768 | 65536 | 131072 | |
| 2n -1 | 7 | 15 | 31 | 63 | 127 | 255 | 511 | 1023 | 2047 | 4095 | 8191 | 16383 | 32767 | 65535 | 131071 |
| 素性检验 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
(向左滑动查看完整表格)
容易看出,若 是合数,则 是合数。它还是 (1) 的推论。设 ,其中 ,则有
另一方面,当 是素数时, 却不一定是素数。例如,对 ,有 .
形如 的素数,称为梅森素数。梅森 (Marin Mersenne, 1588–1648) 是法国一个僧侣,曾与同时代的许多著名数学家(如 Descartes,Fermat,Pascal 等)有交往。1644 年,梅森断言,对于 = 2, 3, 5, 7, 13, 17, 19, 31, 67, 127, 257, 是素数,而对小于 257 的其它 44 个素数, 是合数。后来发现,梅森多算了两个—— 并不会给出素数 ,又漏掉了三个—— 所给出的 都是素数。
目前已经发现的梅森素数共有 51 个。而且,值得一提的是,迄今 (2021 年 12 月 24 日) 为止,已知的最大素数就是一个梅森素数:,它有 24862048 个数位。参见https://primes.utm. edu/largest.html。
练习:设 是正整数且 ,则若 是合数,则 是合数。
3.2 有限几何级数
等幂差公式 (1) 可以重新写成一个更对称的除法形式:
对任意的数 且 以及任意的正整数 ,有
特别地,令 ,就得到:对任意的 ,有
将 (6) 倒过来写一遍,就得到
将 (7) 式中的 换作 (常用字母 ——quotient 的首字母——表示公比,有时也用 ——ratio 的首字母),并乘以一个非零数 (视为数列 的首项),我们得到
(8) 式即等比数列 的前 项和公式,也称有限等比数列的求和公式。它最早以文字的形式出现在 Euclid《原本》第九卷命题 35,参见 [10, p. 69]。它通常出现在高中,但正如 Schmid 和伍鸿熙在《中学代数的主题》一文中所说的 [16, p. 10]:
等比数列的有限求和公式
通常放在高中代数教学近乎结束时,然而我们已经看到,作为符号运用的一个热身,它属于代数最开始阶段。这一推迟毫无理由,特别是考虑到下述因素就更是如此了:因为这个公式在纯数学和应用数学如此多的领域非常重要。
练习 (参见 [12, pp. 11–13]):在
中令
3.3 多项式 除以 的带余除法
由 (1) 式可以立即得到 除以一次多项式 的带余除法:
其中
一般地,对任意的一元多项式 ,我们有以下带余除法等式:
其中 ,而是一个可以根据等式 (5) 算出的多项式。注意,余式 这个结果通常称为余数定理。并且,由此可以推出多项式的根与一次因式的关系(因式定理):数是 f(x) 的根当且仅当 。
3.4 幂函数的单调性
利用平方差公式 (2) 容易证明,平方函数在 (0, ∞) 上单调递增。推而广之,利用等幂差公式 (1) 可以证明,幂函数 (这里 n ≥ 2 是正整数)在 (0, ∞) 上单调递增。我们将它表述为以下引理 [参见 [24, p. 148] 引理 4.6, 它也是 [23, p. 132] 练习 12 的一个简单延伸]:
引理 1 设正整数 ,, ,则
证明:根据等幂差公式 (1),有
注意到,若 , ,则
从而立即得到
即
这就推出 (这里 n ≥ 2 是正整数)在 (0, ∞) 上严格单调递增。证毕。
据此,容易分析出在 (−∞, ∞) 上的单调性。
定理 1 (i) 设 是偶数,,,则 .
(ii) 设 是奇数,, ,则
证明:(i) 设 是偶数,,,则,从而 。
当 , 都不等于 0 时,由引理 1,. 当 , 之一等于 0 时,结论是显然的。
(ii) 设 是奇数。先证充分性:。在 x, y 其中之一等于 0 的情况,由于 是奇数,结论是显然的。以下假定 , 都不等于 0。分三种情况:
• 若 ,则根据引理 1 即得结论。
• 若 ,则由于 是奇数,有,从而 。
• 若 ,则有 ,根据引理 1,就有 。由于 是奇数,这就是,即 。
对于必要性,可用反证法。不然,就有 或 。在前一种情况,根据充分性结果,就有 ,与假设 矛盾;在后一种情况,就有 ,与假设 矛盾。证毕。
定理 1 的第 (ii) 部分有一个有趣的推论,如下:推论:若 是偶数,则对一切实数 , 有
等号成立当且仅当 。
注:值得指出的是,幂函数的单调性(定理 1)是一个中学水平的结果,而无需用到大学微积分中关于可微函数单调性的一般判别准则(导数正 ⇒ 函数增)。其代数基础,正是等幂差公式 (1)。原则上,定理 1 与引理 1 及其证明完全可以下放到初中关于不等式(而无需提及函数及其单调性)的基本讨论中,正如在 的特殊情况下的结果及其证明那样。此外引理 1 中充分性方向的不等式, 可以视为以下一般结果 (可归纳证明) 的特殊情况:设 ,,, 则 .
练习:设 是正整数,,则 .
3.5 幂函数的导数公式
在微积分中,一个基本的结果是幂函数 (这里 是非负整数)在 [0, ∞) 的导数公式 (参见[25, p. 311] 定理 6.16):
它不过是公式 (5) 的一个极限版本。只需注意到, 在 [0, ∞) 连续。根据导数定义,我们有
.
3.6 Bernoulli 不等式
定理 2 (Bernoulli 不等式) 对一切 , 有
并且等号成立当且仅当 .
证明: 根据等幂差公式, 有
.
最后一个不等式成立是因为, 我们有
并且, 容易看出, (13) 式中等号成立当且仅当 . 证毕。
Hirschhorn[8] 曾指出, 上述 Bernoulli 不等式蕴含算术–几何平均值不等式, 这一优美证明也被收入《天书中的数学证明》[1, p. 163], 也参见 [14].
我们指出, 从几何上讲, Bernoulli 不等式断言, 幂函数在第一象限的图像, 在 处的切线落在函数曲线的下方。
3.7 无穷几何级数
提到极限,也许最简单的情况,不是函数的极限而是数列的极限。特别地,对于等比数列的前 项和公式 (9) 取极限(令 n → ∞),就有
注意,对于 ,
. 且此时从而我们得到无穷几何级数公式:
有穷几何级数 (9) 与无穷几何级数 (14),一个是初等数学,一个是高等数学,其分界线是极限(limit) 概念。高等数学高出初等数学的一个体现,就是极限概念。取极限是高等数学里的一句行话。极限有多种表现形式,如函数的极限、导数的概念、数列的极限、无穷级数等,而 (12),(14) 是其代表。Andrews [2, p. 38] 还指出,幂函数 (这里 是非负整数)的定积分公式
也可以由 (14) 得到。从源头上讲,这是不难理解的,因为公式 (14)(在 的特殊情况)首次出现于 Archimedes 求抛物线弓形面积的工作,见 [10, p. 89]。(13) 式也可以从形式幂级数的观点来理解。此时它可以表述为
关于 (14) 式及其变形的种种应用,参见柳柏濂 [13]。
3.8 模 的逆
在等幂差公式 (1) 中令 , ,我们得到 的一个因式分解:
两边在多项式环中取模,得到
这就是说, 模 的逆为。
练习:设方阵 N 满足,其中 m 是正整数,则有.
注:最近,笔者注意到,(17) 的一个推广可用于求解一种特殊类型的微分方程,并确保 Heaviside算子法的有效性。参见 [11, p. 84] 定理 7。
3.9 模 的逆
在 (17) 中令 x = p 为素数,则我们得到
这就是说,在整数环中, 模 的逆为 。(18) 式中的 也可以替换 为一般的正整数 ,只不过这里用 是想提示它与 进数的联系。在 进数中, 也类似于 (15) 式的无穷级数等式成立:
注:进数首先由德国数学家 Kurt Hensel(1861–1941) 在 1897 年发现。Hensel 的出发点,是整数(以及有理数)与复系数多项式(以及复系数有理函数)之间的模拟。整数同余式 (18) 与多项式同余式 (17) 如出一辙,即此模拟的具体体现之一。对此,有兴趣的读者可以参见 Gouvêa [6] 第一章。
3.10 矩阵版本
20 世纪数学的一个显著特征,是从交换到非交换(参见 Atiyah [3])。正如俄国数学家 Shafarevich所说 [17, p. 72],某些理论最自然的“非交换化”推广方法是将数 (numbers) 替换为矩阵 (matrices)。等幂差公式 (1) 也有一个矩阵版本。将表示数的小写字母 , 替换为表示矩阵的大写字母, ,则有:
即
(19) 也称为嵌套 (telescoping) 版本。
1956 年,美国数学家 Peter Lax 基于公式 (19) 证明了 Lax 等价定理。等价定理大致说,对于微分方程的数值求解,兼容性 稳定性 收敛性。在数值分析中,它是数值偏微分方程的根本定理。
2005 年,Lax 荣获 Abel 奖,在挪威科学和艺术学院对其成就的介绍中特别提到了这一工作:
近代数值分析中的另一个基石是“Lax 等价定理”。受 Richtmyer 的启发, Lax 确立了这个定理,它给出了确保数值算法可以有效逼近微分方程解的条件。这一结果照亮了整个领域。
3.11 Fermat 素数
注意到,与立方差公式 (2) 平行的,还有一个立方和公式
公式 (20) 的推广如下:设 是正整数,则有
它只不过是在等幂差公式 (1) 中令 , 并将 替换为 的一个变形。(21) 可称作奇次幂和公式。
根据 (21) 不难看出,对于正整数 , ,只要 含有一个大于 1 的奇数因子 ,则
是合数。因此,要使 对某正整数 , 以及 为素数,就必须要求 不含有大于 1 的奇数因子,从而 是 2 的一个幂。我们考虑一个最简单的情况:, 。此时所考虑的数形如。它有没有可能是素数呢?用计算机测试,列表如下:
| 5 | 6 | 7 | ||||
|---|---|---|---|---|---|---|
| 8 | 16 | 32 | 64 | 128 | ||
| 2 1 | 5 | 17 | 257 | 65537 | 4294967297 | 18446744073709551617 |
| 素性检验 | ✓ | ✓ | ✓ | ✓ |
(向左滑动查看完整表格)
当 n = 1, 2, 3, 4 时,我们确实得到了素数 5, 17, 257, 65537。这引导法国数学家 Fermat 于 1650 年猜测,对一切 n = 1, 2, 3, 4, . . .,都是素数。但 Euler 在 1732 年指出,
从而否定了这个猜想。1880 年,Landry 发现
1975 年,Morrison 和 Brillhart 发现
事实上,目前尚未发现,有某个正整数 使得 是素数。人们倾向于认为与 Fermat 猜测相反的结论成立:对一切 , 是合数。
4 尾声
俄国自学成才的大数学家 I. M. Gelfand (1913–2009) 曾经在不同的场合说 (参见他与 Tatiana V.Gelfand 合著的中学数学教科书2 《几何》之引言):
在知识的领域中,思想 (ideas) 的数目是有限的。其它的一切只是主旋律的种种变奏曲。在数学中,思想并不多。我们所获得的一切,都是从最基本(或根本)的概念 (concepts)出发经过某种程度的变形而得到。掌握一个数学领域中的那些基本概念,有助于将它们与其它领域中的基本概念区分开,有助于将它们应用于其它领域。
Halmos 教授在《数学中有基本元素吗?》[7] 一文中所说的“基本元素”(elements),也许就是主旋律吧。值得一提的是,Halmos 教授所举的三个例子中,头一个就是几何级数 (亦可参见 [15])。他举的每一个例子都很有启发性,推荐给有兴趣的读者。
萧文强教授在《数学可以怎样教得更好?》3[26] 一文中倡导的“少即是多”(Less is More) 的原则,其出发点与此相去不远:以主旋律引领变奏曲。萧教授在附录中也举了一个极其生动的例子,线性方程组的求解。毫无疑问,这也是贯穿小学直至大学数学的一个引人入胜的主旋律。
亲爱的读者朋友,你心中可有一首反复吟唱的主旋律及其变奏曲呢?
致谢
感谢美国加州伯克利大学伍鸿熙教授、香港城市大学陈关荣教授、香港大学萧文强教授、北京师范大学李建华教授、西安电子科技大学张哲博士、北京市朝阳区教育研究中心张浩博士、中国传媒大学陈见柯博士、天津大学刘云朋博士、中国矿业大学(北京)张汉雄博士、陕西西安曲江第一中学雷艳萍老师、浙江永嘉中学叶卢庆老师对初稿提出宝贵意见!
参考文献
[1] M. Aigner, G. M. Ziegler, Proofs from the Book. Sixth Edition. Springer, 2018. 有中译本, 《数学天书中的证明》(第 6 版), 冯荣权、宋春伟、宗传明、李璐译, 北京: 高等教育出版社, 2022.
[2] George E. Andrews, The geometric series in calculus, Amer. Math. Monthly, 105 (1998):1, 36–40.
[3] Michael Atiyah, Mathematics in the 20th century, Amer. Math. Monthly, 108 (2001):7, 654–666.有中译文,白承铭译,二十世纪的数学,数学译林,2002 年第 21 卷,第 1 期,1–14.
[4] G. S. Carr, A Synopsis of Elementary Results in Pure Mathematics, C.F. Hodgson and Son, London, 1880, 1886; reprinted by Chelsea, New York, 1970 under the title, Formulas and Theoremsin Pure Mathematics; reprinted by Cambridge University Press, 2013 under the title, A Synopsis of Elementary Results in Pure and Applied Mathematics.
[5] C. Eckes, Hermann Weyl in Göttingen (1904–1913): The combined impact of Hilbert, Klein and Zermelo, Bhāvanā, Volume 3, Issue 1, January 2019.
[6] Fernando Q. Gouvêa, p-adic Numbers: An Introduction, Third Edition, Springer, 2020.
[7] P. R. Halmos, Does mathematics have elements?. Math. Intelligencer 3(1981), 147–153. 有中译文,陈见柯译,数学有基本元素吗?收入“数学与人文”丛书第三十辑《数学随想》,北京,高等教育出版社,2020.
[8] M. D. Hirschhorn, The AM-GM inequality. The Mathematical Intelligencer 29, 7 (2007).
[9] Robert Kanigel, The Man Who Knew Infinity : A Life of the Genius Ramanujan, 1991. 有中译本,《知无涯者:拉马努金传》,胡乐士、齐民友译,上海世纪出版集团,2008.
[10] V. J. Katz,《数学史通论》(A History of Mathematics: An Introduction), 李文林等译,高等教育出版社,2004.
[11] 林开亮,答薛昭雄教授——并附评论与反思 (续),数学传播,第 44 卷第 4 期(2020 年),78–86.
[12] 林琦焜,从三角求和公式到 Fourier 级数,数学传播,第 26 卷第 3 期(2002 年),11–29.
[13] 柳柏濂,别瞧不起它, 那个中学教材中的公式 ,数学传播,第 22 卷第 2 期(1988 年),63–71.
[14] L. Maligranda, The AM-GM inequality is equivalent to the Bernoulli inequality. The Mathematical Intelligencer, 34 (2012), 1–2.
[15] W. Rudin, Unique right inverses are two-sided. The American Mathematical Monthly, 92 (1985)489–490.
[16] Wilfried Schmid and H. Wu, The major topics of school algebra, 伍鸿熙个人主页, 2008.
[17] I. R. Shafarevich, S. Zdravkovska, Abelian and nonabelian mathematics. Math. Intelligencer 13,67–75 (1991). 有中译文,潘建中译,交换数学与非交换数学,数学译林,1992 年第 11 卷,第 2期,94–104.
[18] Abe Shenitzer, Teaching mathematics, Math. Intelligencer, 3 (1981), 109–114.
[19] André Weil, Two Lectures on number theory, past and present, L’Enseignement Mathématique,20: 87–110, 1974. 有中译文,王启明译,数论今昔两讲,数学译林试刊,1981 年 83–90.
[20] H. Wu, Understanding Numbers in Elementary School Mathematics, American Mathematical Society, 2010. 有中译本,赵洁、林开亮译,《数学家讲解小学数学》,北京,北京大学出版社,2016.
[21] H. Wu, Teaching School Mathematics: Pre-Algebra, American Mathematical Society, 2016.
[22] H. Wu, Teaching School Mathematics: Algebra, American Mathematical Society, 2016.
[23] H. Wu, Rational Numbers to Linear Equations, American Mathematical Society, 2020.
[24] H. Wu, Algebra and Geometry, American Mathematical Society, 2020.
[25] H. Wu, Pre-Calculus, Calculus, and Beyond, American Mathematical Society, 2020.
[26] 萧文强,数学可以怎样教得更好?,数学传播,第 40 卷第 1 期(2016 年),81–86.
[27] 杨振宁,量子化、对称和相位因子:20 世纪物理学的主旋律,收入《杨振宁的科学世界:数学与物理的交融》,季理真、林开亮主编,北京,高等教育出版社,2018 年。
——本文作者林开亮任教中国西北农林科技大学理学院