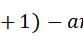【4】利用拉格朗日中值定理证不等式
在近几年的数学高考中,出现了不少含有拉格朗日中值定理的试题.常以不等式恒成立问题为基本切入点,具有一定的深度,既符合高考命题“能力立意”的宗旨,又突出了数学的学科特点,较好地甄别了学生的数学能力. 下面以近几年全国各地的数学高考试题为例,说明拉格朗日中值定理的不同形式在高考中不等式的应用,更好地体会用“高等数学”知识解题的优势.
用拉格朗日中值定理证明不等式的步骤:

具体案例如下所以:


评注:这道题用初等数学的方法证明较为冗长,而且技巧性较强.因而思路较为突兀,大多数考生往往难以想到.相比之下,用拉格朗日中值定理证明,思路较为自然、流畅.体现了高观点解题的优越性,说明了学习高等数学的重要性.