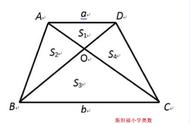
在小学奥数面积六大模型中,以动物命名的模型有3个,蝴蝶模型、鸟头模型和燕尾模型,蝴蝶模型应用于四边形,鸟头模型和燕尾模型应用于三角形。同样应用于三角形,鸟头模型是共角三角形,而燕尾模型是共底三角形,也就是说,两个底相同的三角形分布于以底为分界线的两侧,形状像燕子的尾巴,故得名燕尾模型(燕尾定理)。

一、燕尾定理
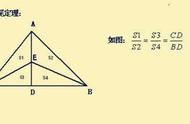
★在三角形 ABC 中, AD , BE , CF 相交于同一点 O ,那么:
❶S△AOB:S△AOC= BD : DC

★推广:
❷S△AOB:S△BOC=AE:EC
❸S△AOC:S△BOC=AF:FB
二、定理证明
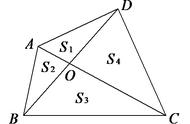
以❶S△AOB:S△AOC= BD : DC 为例,说明一下燕尾定理的证明过程。

根据等高三角形面积之比等于对应底之间之比的性质,
S△BOD:S△COD=BD:DC①
同理,S△BOD:S△AOB=S△COD:S△AOC=OD:AO②
由②得,S△AOB:S△AOC=S△BOD:S△COD
由①得,S△AOB:S△AOC=S△BOD:S△COD=BD:DC
从而❶S△AOB:S△AOC= BD : DC得证,❷❸同理可证。
三、记忆方法

以❶S△AOB:S△AOC= BD : DC为例,我们发现以△AOB和△AOC是共底三角形,而且两个三角形分布于底的两侧,两个三角形除底之外的第三个顶点得连线被底所在直线所截,分成两部分(BD和CD),可得两个三角形面积之比等于被底所截两线段之比。
简记为:共底三角形面积之比,等于第三点连线被底所截线段之比。
四、燕尾定理应用
上述定理给出了一个新的转化面积比与线段比的手段,在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的途径。