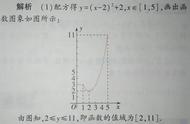
确定出对对数放缩时为什么将lnx放缩成x/2,因为主元为一次函数,还要保证放缩之后的函数单减,因此一次函数系数要为负值,此时也可将lnx放缩成x/k,只要保证0<k<1即可,如果对刚才经验取点法不熟悉,也可用放缩取点法证明函数在0<x<1上存在一个零点,过程如下:


注意案例3中确定出需对lnx放缩,但为什么放缩成根式形式,因为函数中-2ax为主元,它决定函数整体的趋势,因此需要将lnx放缩成一个速率小于-2ax的形式,这样放缩后的趋势也不改变,所以需要把lnx放缩成一个幂函数,且幂指数小于1方可。

案例4中虽然ex为主元,可对一次函数-ax进行放缩,但由于不确定x的上界,将-ax放缩成一个数字时符号是反的,此时可对主元放缩,且放缩后依旧为主元,因为-ax为一次,因此可将ex放缩成比1次要高的幂函数,即ex>x²