第二章间接证明法

证明面积相等三大方法
☞适用条件:当未知图形与已知图形类型相同(都是三角形或都是平行四边形),但彼此的底和高的大小关系不确定。备注:正方形和长方形也属于平行四边形。
☞判断方法:通过以下方法可证明其面积相等。
❶割补法。当未知图形与已知图形同时割去或者添补上相同面积的图形后,形成的新图形如果面积相等,那么未知图形与已知图形面积相等。
☞同时割去相同面积的图形(或者同一图形)。
★用字母表示为:若S1-S=S2-S,则S1=S2
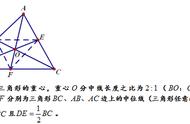
如图所示,三角形DBC面积为6cm²,已知三角形DEC和三角形AEB面积相等,求三角形ABC面积是多少?

我们观察后发现,三角形ABC和三角形DBC同时割去三角形BEC后,得到的新图形三角形DEC和三角形AEB面积相等,因此三角形ABC和三角形DBC面积相等,都为6cm²
☞同时填补上相同面积的图形(或者同一图形)。
★用字母表示为:若S1 S=S2 S,则S1=S2
如图所示,图中是两个完全相同的直角三角形叠在一起,求阴影部分面积?

所求阴影部分是个梯形,如果我们利用梯形面积公式去求,因缺少上底、下底和高的值,不能直接求解。但我们如果利用添补法,③面积 ②面积之和为三角形DEG面积,①面积 ②面积之和为三角形ABC面积,由此可得,可以证明阴影面积=梯形ABEF面积,就找到了解题思路。
❷转换法。当未知图形与已知图形都与第三个图形面积相等时,那么未知图形与已知图形面积相等。
★用字母表示为:若S1=S,且S2=S,则S1=S2
如图,在四边形ABCD中,P是边AB的中点,在BC边上取一点E,使三角形BED的面积与三角形PBD的面积相等,已知三角形BED的面积为5cm²,求阴影部分面积。

因为,P是边AB的中点,所以,AP=PB,三角形APD与三角形PBD等底同高,二者面积相等。又因为三角形BED的面积与三角形PBD的面积相等,所以,三角形APD的面积与三角BED的面积相等,为5cm²。
☞练习题
如图所示,在三角形的斜边上任取一点,向两条直角边上做垂线,相应的边长如图所示,求阴影部分面积。(答案附评论区)