不少同学都已经开始了期末复习,同学们复习的时候可以查看前面甜甜老师总结过的知识点,也可以使用之前的测试卷做复习检测,甜甜老师也会陆续分享期末综合卷。
今天先来把《圆》这一单元的第二个重点:圆的面积及其应用相关知识点和常考、必考题型总结一下。
一、圆的面积公式及其推导过程
1、把一个圆平均分成若干偶数等份,再通过拼接的方式将其拼接成一个近似的长方形。
这个长方形的长相当于圆的周长的一半【C÷2=πr】,长方形的宽相当于圆的半径【r】。
那么圆的面积=长方形的面积=长×宽=πr·r。

2、根据圆的面积公式可以推出,只要只要圆的半径或直径,就能计算出圆的面积;
反之,只要知道圆的面积,就能计算出圆的半径和直径;
或者已知圆的周长,也可以先计算出直径或半径,然后在计算面积。
具体公式整理如下:

3、半圆的面积:半圆的面积=圆的面积÷2=πr·r÷2。
4、圆环的面积=外圆面积-内圆面积=πR·R-πr·r=π(R·R-r·r)

5、圆环的环宽(L)与内圆半径(r)、外圆半径(R)之间的关系:
环宽 内圆半径=外圆半径;外圆半径-环宽=内圆半径。

类型一、与圆的面积公式推导过程有关的题型
【例1】、把一个圆平均分成若干偶数等份,再拼成一个近似长方形,已知圆的半径是4厘米,那么长方形的长是多少?
【解析】考察面积公式的推导过程,长方形的长相当于圆的周长的一半=πr。
r=4cm,所以长=3.14×4=12.56cm
【总结】:面积公式的推导过程,一定要牢记【长方形的长=πr,宽=r】
【例2】、把一个圆平均分成若干偶数等份,再拼成一个近似长方形。量出长方形的长是12.56
厘米,这个圆的面积是多少平方厘米?
【解析】已知长方形的长=πr=12.56,那么r=12.56÷3.14=4cm;
圆的面积=3.14×4×4=50.24平方厘米。
【例3】、在推导圆的面积公式时,将圆等分成若干份,拼成一个近似的长方形,已知长方形的长比宽多6.42厘米,圆的面积是多少平方厘米?
【解析】长方形的长=πr,宽=r,已知长方形的长比宽多6.42厘米,
也就是πr-r=r(π-1)=2.14r=6.42,可求出r=3cm。
那么圆的面积=3.14·3·3·=28.26平方厘米。
【例4】、把一个圆平均分成若干份,拼成一个近似的长方形,拼成的长方形的周长比圆的周长多8厘米,这个圆的面积是多少平方厘米?
【解析】长方形的长=πr,宽=r,所以长方形的周长=(πr r)×2=2πr 2r,圆的周长是2πr。
已知长方形的周长比圆的周长多8厘米,也就是2πr 2r-2πr=2r=8cm,所以r=4cm。
圆的面积=3.14×4×4=50.24平方厘米。
【总结】面积公式的推导过程,一定要牢记【长方形的长=πr,宽=r】。
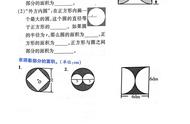
【例5】、把一个圆平均分成若干份,拼成一个近似长方形。若圆的面积是50.24平方厘米,阴影部分的面积是( )平方厘米。

【解析】、把圆重新拼成长方形的过程中,圆的面积=长方形的面积=50.24平方厘米。
阴影部分的面积=长方形面积-1/4圆的面积=圆的面积=1/4圆的面积=50.24-50.24×1/4=37.68平方厘米。
【提示】、这类题型要把握好圆的面积公式推导过程中,圆和长方形之间的关联,解题就非常简单。当然,先算出圆的半价,再计算长方形的面积也可以,只不过过程比较麻烦。
类型二、圆的面积与实际问题相结合
【例6】、一个圆形花坛,直径是20米,在它的外围修一条宽2米的石子小路,这条小路的面积是
多少平方米?
【解析】、求圆环的面积,r=20÷2=10米,R=10 2=12米;
圆环的面积=3.14×(12×12=10×10)=138.16平方米。
【总结】、在圆形物体的外围修路、铺草坪,形成的就是圆环,路宽就是环宽,直接用圆环面积公式计算即可。
【例7】、有一个环形铁片,它的内圆周长是62.8厘米,外圆周长是94.2厘米,这个铁片的面积是多少平方厘米?
【解析】要求环形的面积,需要知道外圆半径和内圆半径,所以先根据周长算出半径。
内圆半径=62.8÷3.14÷2=5厘米;外圆半径=94.2÷3.14÷2=15厘米;
所以圆环面积=3.14×(12×12=10×10)=138.16平方厘米。
【例8】、将一个半径5厘米的圆形铁片,加工成半径为4厘米的圆形铁片零件,铁片的面积减少了多少平方厘米?
【解析】原来铁片半径5cm,加工后变成4cm,那么减少的部分就是一个宽度为1cm的圆环,直接用圆环面积公式计算即可:
减少的面积=3.14×(5·5-4·4)=28.26平方厘米。
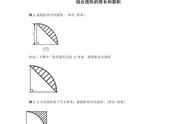
圆的面积还有两类类重点也是难点题型,一是把圆(或圆环)和正方形、三角形结合在一起;二是求阴影部分的面积。
这两种题型相对来说比较灵活一些,需要积累一些小技巧和解题方法,甜甜老师下次再梳理。大家可关注一下。
,