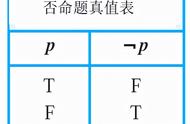
一.命题:一般地,我们把用语言、符号或式子表达的,可以判断真假的陈述句叫做命题。
判断真的语句叫做真命题
判断假的语句叫做假命题
初中数学中的许多命题可以写成“若p,则q”的形式,“如果p,那么q”等形式,其中p称为命题的条件,q称为命题的结论。
例.把下列命题写成“若p,则q”的形式,并判断其真假.
(1)三边对应相等的两个三角形全等;
(2)末位数字是0的整数是5的倍数;
(3)两条对角线相等的四边形是矩形.
【解答】解:(1)若两个三角形的三边对应相等,则这两个三角形全等.它是真命题,
(2)若一个整数的末位数字是0,则这个整数是5的倍数.它是真命题,
(3)若四边形的两条对角线相等,则这个四边形是矩形.它是假命题.
二.充分条件与必要条件
一般地,“若p,则q”为真命题,是指由p通过推理可以得出q,这时,我们就说,由p可以推出q,记作pq,并且说,p是q的充分条件,q是p的必要条件。
如果“若p,则q”为假命题,那么条件p不能推出结论q,记作p⇏q,此时,我们就说p不是q的充分条件,q不是p的必要条件。
例.(2022春•嘉兴期中)已知a,b为实数,则“a3<b3”是“a<b”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【分析】利用函数y=x3的单调性,结合充分条件和必要条件的性质判断即可.
【解答】解:函数y=x3在R上单调递增,则a3<b3⇔a<b,
则“a3<b3”是“a<b”的充要条件,
故选:C.
【点评】本题考查充要条件,属于基础题.
充要条件:

例: