观测者A认为这个事件经历的时间更长,这就是所谓的“时间膨胀”,这个公式是洛伦兹变换的一个推论。
(关于洛伦兹变换,各位读者可以参考笔者之前的作品,评论区里会附上链接。)
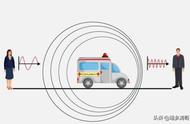
把这个结论用到波源绕着观测者做圆周运动的情景中(观测者绕着波源做圆周运动的情景也一样),观测者会发现声源振动的周期变长了,这就使其测到的声波频率也变小了。

这就是“横向多普勒效应”,是时空本身的属性,这种频率变化只与声源和观测者的相对运动速度的大小有关,与它们相对运动速度的方向是没有关系的。
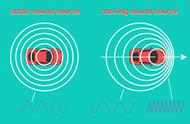
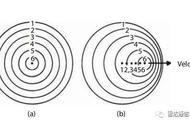
之前讨论的一大堆波源和观测者之间的距离随时间变化的情景也可以被称为“纵向多普勒效应”。
没错,发生“纵向多普勒效应”的时候也会掺杂着“横向多普勒效应”(时间膨胀),你可能已经猜到了修正“纵向多普勒效应”公式的方法:

这就是修正后的描述声波多普勒效应的“统一公式”,声波的各种多普勒效应都可以由这个公式统一地描述!
光波,这才是动静等观!提及多普勒效应,肯定绕不开光波的多普勒效应。提及绝对空间与相对空间,更是绕不开光波的多普勒效应。
知道了描述声波多普勒效应的公式,描述光波的多普勒效应就已经不是什么难事了。
我们只需要知道“光速不变”,不管是光源运动还是观测者运动,观测者测到的光速都不变。也就是说,光波的多普勒效应只由波长的变化引起。
那么,这里的运动是相对于谁运动?可以类比声波,认为是相对于光波的介质静止吗?
你可能已经发现了“光速不变”让光源运动与观测者运动变得“不可区分”了。不管是哪一方运动,描述光波多普勒效应的公式都是一样的。
我相信你可以完成下面的操作:

没错,这就是描述光波多普勒效应的“统一公式”,光波的各种多普勒效应都可以由这个公式统一地描述!
如果光源和观测者相互远离,只需要把上面公式里的光源速度或观测者速度取成负值就可以了。
有些人还搞了一些操作,把公式变了个形式: