第58回
以斜制邪,八角莲台河中立
长桥栈道,春光无限别样情
话说唐僧准备打道回府被八戒一声"且慢"叫停了下来.
"既然枯井是虚设的,那我们把枯井假设在大树P的位置不可以吗?"八戒问道。

"当然可以,而且还更容易找到宝贝."悟空说,"如图1,把大树的位置点P看做是枯井的位置,从点P走到大树Q的位置,左转走到点A(即∠PQA=90°),使QA=PQ.连接PA,则PA的中点E就是藏宝的位置."
"太神奇了!"八戒按照悟空的方案尝试着,结果发现PA的中点E与原来藏宝的点O确实是同一个点.
"这没啥奇怪的呢,八戒。一般的可以成立,特殊的当然也成立了。"师父说完催促道,"天快黑了,大家都快点回去吧."
翌日,大桥指挥部决定在大桥的上游紧挨大桥的河中建一个八角莲花台,把金狮子安置在莲花台上,四周用铁栏栅围住.这样一来不仅让莲花台成为流沙河上一道亮丽的风景线,又能让众人瞻仰金狮子的风采.
自从找到了金狮子,建桥工程进展非常顺利,数月之后大桥和八角莲花台同时竣工,择日剪彩通车。
大桥通车剪彩这一天,指挥部特邀唐僧师徒上八角莲花台祭祀。祭祀时需要从河里取3升的河水备用,唐僧吩咐三个徒弟下河取水,并强调说河水一定要取3升,不能多,也不能少(当然,微小误差是可以的)。
"师父,没有3升的容器怎么取3升的水啊?"八戒找遍了莲花台也没找到3升的容器,"只有两只容量分别6升和5升的大葫芦,怎么办呢?"
"你们自己去想办法吧。"
"沙师弟,你去买个容量刚好3升的容器来。"八戒对沙僧说。
"不用啦沙师弟。八戒,你带上这两只葫芦跟我下河。"悟空说完走下莲花台。
"猴哥,就这两只葫芦能取回3升的水吗?"八戒说,"师父可说过了,取回的水一定要是3升。"
"没问题的八戒。"悟空胸有成竹。
"我看你怎么取?"八戒将信将疑,带着葫芦跟在悟空、沙僧的后面。
三人走到河边,悟空开始对八戒和沙僧发号施令。
"八戒,你把5升的葫芦给沙师弟,然后你把6升的葫芦装满。"
"装满了大师兄。"八戒装满了水。
"你把水倒入沙师弟的葫芦,倒满为止,小心不要把水漏掉。"
"倒满了,猴哥。"
"沙师弟,把你葫芦里的水倒进河里。"
"八戒,把你葫芦里剩下的1升水倒进沙师弟的葫芦里。"
"猴哥,我知道然后取回3升水了。"八戒恍然大悟。
接下来只见八戒和沙僧两人进行了如下操作:
八戒用6升葫芦装满水,然后倒进沙僧还可装4升水的葫芦里,倒满后,沙僧把葫芦里的水倒掉,八戒把葫芦里剩下的2升水倒进沙僧的葫芦里;
八戒又装满葫芦6升水,然后倒进沙僧还可装3升水的葫芦。
"猴哥,我这葫芦里的水刚好是3升。"
兄弟三人取回3升的河水。
祭祀完毕后,唐僧发现莲花台的四周没有安上围栏,存在着安全隐患,要是小孩上去追逐嬉闹,掉下河去的危险性很大。
师父让八戒去度量一下这个莲花台的周长,以便明日去购买围栏材料回来装上。
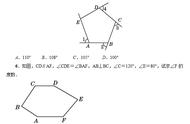
八戒绕着莲花台四周走了一圈,发现这个莲花台是个八边形ABCDEFGH,八个角虽然都相等,但各边的长却明显不全相等。
八戒觉得甚是奇怪,跑去问唐僧道:"师父,您说这个莲花台怎么是斜八边形,而不是正八边形呢"
"这你就不懂了."唐僧说,"这叫做以斜制邪!"
回到住所,沙僧向八戒问道:"二师兄,师父吩咐你量得的那个八角莲花台的各边长如何?"
八戒掏出绘制好的如图2递给沙僧,说:"你看,全在这。"

沙僧接过来一看,这是一个各角都相等的八边形,在图的底行写着:AB=7,BC=4,CD=2,DE=5,EF=6,FG=2(单位:米).
"二师兄,你怎么才量得六边的长啊?"沙僧问道,"还有GH和HA这两边的长呢?"
"是吗?可能是边数太多漏掉了。"八戒说,"要不我连夜再过去补量一下吧?"
"八戒,你办事怎么还是那样毛手毛脚啊!"师父嗔怪后又疼爱地说,"这么晚就别去了,明天再去吧。"
"给我看一下。"悟空接过沙僧递过来的图纸看了一下后说,"不必去了,漏掉的两边GH和HA可以求出来的."
"可以求出来吗?"沙僧不解。

"是的。幸好八戒量得八个角的度数都相等。否则就无法求解了."悟空说,"你们看,如图3,由于八边形的每个内角都是135°,所以每个外角都是45°,联想到等腰直角三角形,只需要分别把边BC、DE、FG、HA向两端延长,交于点M、N、P、Q,则△MAB、△NGH、△PEF和△QCD都是等腰直角三角形,所以∠M=∠N=∠P=∠Q=90°,四边形MNPQ是矩形,所以MN=PQ,MQ=NP。
设AM=BM=x,因为AB=7,由勾股定理,得:
x2 x2=49,2x2=49,x2=49/2,x=7√2/2,
所以AM=BM=7√2/2;
同理,CQ=DQ=√2,
EP=FP=37√2,
由MQ=NP,得:BM BC CQ=FP FG GN,
即7√2/2 4 √2=3√2 2 GN,
所以GN=3√2/2 2,
所以GH=
GN=√2(3√2/2 2)=3 2√2;同理,由MN=PQ,得HA=3 √2。
所以,八边形的周长为32 3√2(米).
安上护栏的八角莲花台赢得了沙河市民的好评和点赞,大家一致称赞唐僧佛祖心肠。唐僧为了在当地百姓留下更美好的口碑,他干脆好人做到底,建议沙僧用造桥节省下来的一笔钱在流沙河宽阔地带的沙滩上根据地形造一个人工湖。
沙僧听从师父的建议,征得建桥指挥部的同意后工程如期开工。
人工湖建成后的一天,师父带着悟空、八戒重游流沙河,沙僧带着他们三人游览人工湖。

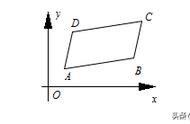
"师父,数月前按照您的吩咐,人工湖本来打算建成圆形的,但由于地形地貌的限制,最后只能挖成一个菱形。"沙僧指着如图4的图纸说,"这就是人工湖的示意图,它的岸边是菱形ABCD,边长为200米,∠A=120°.对角线BD是一座长桥,湖的四周铺上木栈道,栈道外种花插柳,如今已是杨柳低垂,百花争艳.每当夜幕降临,长桥上、栈道边成为了少男少女们山盟海誓约会的好场所,同时也是中老年人休闲的好去处."
师徒四人沿着湖中的长桥走,桥下荷花绽放,鱼儿悠闲。走到半道时,悟空突然问道:"沙师弟,何不在这桥BD上再建两条可晃荡的索道通向湖的对岸BC和CD呢?"
"猴哥,建这个索道有什么用呢?"八戒问。
"现在的小孩和年轻人都喜欢刺激冒险,为满足他们的好奇心理嘛。"悟空答。
"大师兄,你说的没错,许多年轻人曾多次向我提过这样的设想和要求,我也答应过他们,并说如果造价超过18万就得缓一缓。"沙僧说,"建这两条索道给出的报价是每米长1000元。"
"那你就得想办法使这两条索道总长最短。"八戒说,"这个问题转化为数学问题就是:已知菱形ABCD,K是对角线BD上的点,求K到BC、CD的距离之和KP KQ的最小值。"
"是的,二师兄。"沙僧说,"算出了索道的最短长度,就能确定造价是否会超过18万?可是我无法确定这个最小值究竟是多少?"
"猴哥,这里的三点K、P、Q都不确定,如何确定KP KQ的最小值呢?"
"我记得类似的问题解过不少,"沙僧说,"好像都是需要先以直线为对称轴把两个动点中的一个变换到另一边去."
"好记性啊,沙师弟."悟空说,"对,解决动点线段和最短路线问题常常使用这一招.由于BD是菱形的对称轴,以它为对称轴把点P变换到AB边上,记为点E,连接KE,QE(如图5),则KP=KE,因此,KP KQ=KE KQ≥EQ,所以,要使KP KQ最短,只需要EQ 最短."

"E、Q都是动点,如何才能使EQ最短呢?"八戒问.
"注意到E、Q在平行线AB、CD上,"悟空说,"根据'平行线间的距离是这两条平行线上任何两点之间距离的最小值'可知:EQ的最小值就是AB、CD之间的距离."
"如何求AB、CD之间的距离呢?"八戒问。
"连接AC,则四边形ABCD是菱形及∠A=120°,得∠ABC=60°,△ABC是等边三角形,
作CF⊥AB,则BF=AB/2=100,
所以CF=√(40000-10000)=1007√3.
所以AB、CD间的距离为100√3米,
所以,两条铁索桥的总长最短为100
米,约等于173米,所以需要最省的造价约为17.3万元."
"沙师弟,可以开工了。"
"是的二师兄,既然最低造价不超过18万,明天就可以工程队签订合同了。"
欲知后事如何?请看下回分解.
,