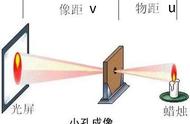
孔越小,效果越好
在课堂上第一次接触光学的时候,为了说明光的直线传播原理,老师往往会给我们演示一个实验:取一个开有小孔的黑匣子,让小孔对着外面阳光下的物体,物体就会在匣子后壁投下一个清晰的倒像。当然,为了能看到这个像,通常要把后壁去掉,代以蒙上一张半透明的纸。
这就是著名的小孔成像实验,在历史上,它是由我国战国时代的伟大思想家墨翟最早提到的。在西方中世纪,人们甚至设计了一些没有窗户的屋子,四壁只留一个小孔让光线透进来,当白天人走进屋子,关上门后,远处群山、塔楼的倒像就赫然出现在墙壁上。
在小孔成像实验中,要想让图像清晰,孔必须要小。因为孔越大,图像就越模糊。譬如说,假如你在乡下拥有一间窗户正对着远处群山的房间,那么白天你或许也能在粉壁上看到远处群山的模糊倒影。其图像质量之所以不好,就是因为窗户比起小孔来太大。
为什么孔越大图像越模糊呢?因为在孔大的情况下,光线太发散,从同一物体上部和下部投来的光线,在壁上相互重叠在一起,图像自然就变得不清晰了。为了验证这一点,你自己不妨在纸上画画看:当小孔是一个理想的点时,物体上下部所投的像是完全分开的;当孔的尺寸稍变大,两部分像开始有点重叠;孔越大,重叠得就越多;直至最后全部重叠在一起,这时也就谈不上有什么像了。

让窗户小孔成像
但是,最近美国麻省理工的两位计算机科学家发明了一种新的处理技术,甚至能让像窗户那么大的“孔”也能成一个比较清晰的像。
设想远处有一棵树,通过窗户在房间墙壁上成一个模糊的倒像。用数码相机拍摄下这个像,我们称其为甲。
现在,在像前面放一个不透明的障碍物,障碍物在墙上留下一块阴影。调整障碍物的位置,使树的像完全笼罩在该障碍物的阴影之下。再用数码相机拍摄下墙上障碍物的影子,我们称之为乙。
在电脑上,用软件把照片甲减去照片乙。这时你会惊讶地发现,相减留下的照片中,树的倒像忽然变清晰了许多。
为什么这么一来倒像就会变清晰?让我们先比较一下甲乙两张照片有何不同:甲照片拍摄下的是所有透过窗口投射到墙壁上的光线;而乙照片拍摄下的光线,除了一部分光线被障碍物挡住外,其余的跟甲完全一样;甲减去乙,意味着两张照片中共有的光线相消,得到的将是那部分被障碍物挡住的光线。这部分光线的发散程度显然比光线原先从整个窗户透进来时要小多了。这其实相当于成像所用的“孔”由一扇窗户变成了一个障碍物;孔的尺寸缩小了,所成的像自然就更清晰了。
为了让你能够理解这一点,我们拣一束从窗户照进来,在障碍物上擦身而过,最后投影在树的倒像上的光线,看看它经上述方法处理后的“命运”如何。倘若上述处理的确等价于以障碍物为小孔的成像,那么因这束光线在“小孔”之外,对像的清晰度只会起干扰作用,所以最后理应被消去。
在甲中,这束光线投在树的倒像上。在乙中,这束光线依然投在树的倒像上,只不过此时树的像被障碍物的像罩住了。这束光线在两张照片中同时出现,那么一相减,诚如我们所料,这束光线就被消去了。
既然在这项技术中,障碍物充当了小孔,那么要想得到更清晰的像,我们只须放置更小的障碍物就可以了。但障碍物也不能太小,因为这样处理的前提是原先树通过窗户所成的像必须被障碍物的影子盖住,所以,障碍物的影子不得比这个像更小。
在该项发明中,科学家用到了两张数码照片相减的技术。不知关注当代科学发展的读者是否还记得,2011年获得诺贝尔物理学奖的成果——发现宇宙在加速膨胀——中也用到过该技术:测量宇宙膨胀速度的一个关键是寻找更多的超新星。但超新星尽管亮度很大,可惜因为距离我们遥远,依然湮没在璀璨的星空中,凭肉眼是很难发现的。不过超新星有个与众不同的特点,别的恒星在短时间内亮度不会发生明显的变化,而超新星的亮度变化非常剧烈。利用这一特点,天文学家让同一天区在时间上一前一后拍摄的两张数码照片相减,假如那片天区要是有超新星,那么在亮度相消之后,就会暴露出来。
你看,数码技术不仅可以协助我们处理海量的数据,还可以为我们提供新的研究方法。
,