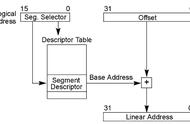
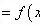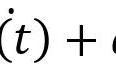什么是线性相关呢?
我们随便看个矩阵:

这个矩阵,乍一看上去能构成一个斜角坐标系,也就是基底i'=(1,2),j'=(2,4)的斜角坐标系,然而,当你实际去画的时候,发现这“矩阵”实际上只是一维坐标,因为这两个基底向量重合了,只是差了2倍:

所以我们就说i'=(1,2)和j'=(2,4)这俩向量线性相关。再进一步,我们拿个三维空间里面随便两个向量a和b,只要你说:

这两个向量就是共线的,它就是所谓的 “线性相关“。至于这个k是正还是负,是整数还是无理数,都无所谓,因为它们在一条线上。如果它们俩构成一个矩阵,那么自然要降低一个维度,也就是说该矩阵是“不满秩”的。(当然,如果你不理解什么是秩,那也没关系,本文并不打算讲清楚它)