【规律方法】
1.把所提供的平面图形拆分成若干个三角形,然后在各个三角形内利用正弦、余弦定理求解.
2.寻找各个三角形之间的联系,交叉使用公共条件,求出结果,求解时要灵活利用平面几何的性质,将几何性质与正弦、余弦定理有机结合起来.

【反思与感悟】
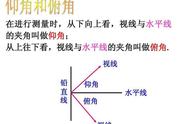
利用解三角形解决实际问题时:(1)要理解题意,整合题目条件,画出示意图,建立一个三角形模型;(2)要理解仰角、俯角、方位角、方向角等概念;(3)三角函数模型中,要确定相应参数和自变量范围,最后还要检验问题的实际意义.
【易错防范】
在三角形和三角函数的综合问题中,要注意边角关系相互制约,推理题中的隐含条件.