三角形内角和定理证明方法四:
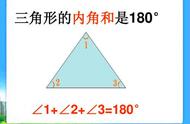
已知:△ABC的三个内角是∠A,∠B,∠C.求证:∠A ∠B ∠C=180°.

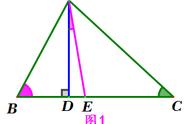
证明:作BC的延长线CD,在△ABC的外部以CA为一边,
CE为另一边画∠1=∠A,于是CE∥BA,
∴∠B=∠2
又∵∠1 ∠2 ∠ACB=180°
∴∠A ∠B ∠ACB=180°

三角形内角和定理证明方法五:
已知:△ABC的三个内角是∠A,∠B,∠C.求证:∠A ∠B ∠C=180°.

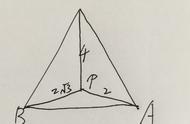
证明:在BC上任取一点D,作DE∥BA交AC于E,
DF∥CA交AB于F,
则有∠2=∠B,∠3=∠C,∠1=∠4,∠4=∠A
∴∠1=∠A
又∵∠1 ∠2 ∠3=180°
∴∠A ∠B ∠C=180°