三角形内角和定理证明方法六:
已知:△ABC的三个内角是∠A,∠B,∠C.求证:∠A ∠B ∠C=180°.

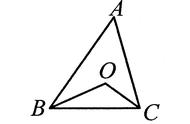
证明:(1)选点O在△ABC内,则如图所示,
过点O分别作DE//AB,FG//BC,PQ//AC,即得:
∠POE=∠GPO=∠A,
∠POG=∠EFO=∠C,
∠EOF=∠PGO=∠B,
∵∠POE ∠POG ∠EOF=180°,
∴∠A ∠C ∠B=180°.

三角形内角和定理证明方法七:
已知:△ABC的三个内角是∠A,∠B,∠C.求证:∠A ∠B ∠C=180°.

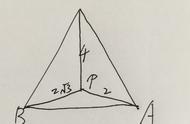
证明:若选点O在△ABC上且不为顶点,则如图所示,
过点O分作OQ//AC, OF//BC , 即得:
∠A=∠BOQ,∠C =∠OQB=∠QOF,∠B=∠AOF ,
∵∠BOQ ∠QOF ∠AOF=180°,
∴∠A ∠C ∠B=180°.