〔6〕删除相关的候选数。

〔5〕观察第六宫
在第六宫中,数字59有两种填法:
第一种填法:r5c1=5、r5c3=9。
第二种填法:r5c1=9、r5c3=5。
〔6〕数对r5c13(59)的多解区在第二宫和第五行。
〔7〕结论:宫行数对(ab)的多解区是数对所在的宫和行。
其中:数字a的多解区是数对所在的宫和行,数字b的多解区是数对所在的宫和行。构成数对的两个单元格是多解格,两格互为多解格。
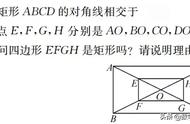
三、举例说明什么是唯一矩形

实例一
〔一〕观察这四个单元格:r3c1、r3c3、r6c1、r6c3。
〔二〕假如r6c1≠5时,再观察这四个单元格。

1、观察单元格r3c1
〔1〕第三宫中有一组数对r3c13,那么单元格r3c1在第三宫和第三行上是多解格。
〔2〕第一列上有一组数对r36c1,那么单元格r3c1在第一列上是多解格。
〔3〕所以单元格r3c1在第一宫、第三行和第一列上都是多解格,所以单元格r3c1是全盘多解格。
2、观察单元格r3c2
〔1〕第三宫中有一组数对r3c13,那么单元格r3c2在第三宫和第三行上是多解格。
〔2〕第三列上有一组数对r36c3,那么单元格r3c2在第三列上是多解格。
〔3〕所以单元格r3c2在第一宫、第三行和第三列上都是多解格,所以单元格r3c2是全盘多解格。
3、观察单元格r6c1
〔1〕第四宫中有一组数对r6c13,那么单元格r6c1在第四宫和第六行上是多解格。
〔2〕第一列上有一组数对r36c1,那么单元格r6c1在第一列上是多解格。
〔3〕所以单元格r6c1在第四宫、第六行和第一列上都是多解格,所以单元格r3c1是全盘多解格。
4、观察单元格r6c3
〔1〕第四宫中有一组数对r6c13,那么单元格r6c2在第四宫和第六行上是多解格。
〔2〕第三列上有一组数对r36c3,那么单元格r6c3在第三列上是多解格。
〔3〕所以单元格r6c3在第四宫、第六行和第三列上都是多解格,所以单元格r6c3是全盘多解格。
5、结论:假如r6c1≠5时,r3c1、r3c3、r6c1、r6c3都是多解格。也就是说候选数23在单元格的填法不是唯一的。四格在一起才形成全盘多解,四格互为多解格。
〔三〕假设r6c1≠5时,通过试数法来研究。
1、假设r3c1=1时