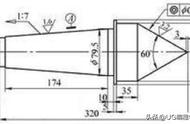
图2 锥度循环

图3 简单螺纹循环
车削多头螺纹可用退刀的办法解决。如图5,以A点作为第一头螺纹的起点,当经过适当次循环后车好第一头螺纹后,把刀尖从A点退到G点作为第二头螺纹的起点,C点位置不变;依此类推,即可车削多头螺纹。设导程为F,螺纹头数为M,则每头的退刀距离为:H=F/M,并用H值编制退刀程序,这样就可以加工出多头螺纹。

图4 螺纹行程

图5 多头螺纹的转换
锥螺纹循环基本上与图3所示柱螺纹循环相同,只是图中的BC段为螺纹的锥度(斜线)。
简单螺纹切削方式由于每次推进量I为固定值,即每次的切削剖面不等,是不合理的,不是理想的螺纹切削方式,所以称为简单螺纹循环。
4.复杂螺纹循环:G⊿⊿
复杂螺纹循环与简单螺纹循环相比,其主要特点是每次进刀深度是递减的,并且按一定规律由数控系统自动分配,其次是60°刀刃切入时,基本上是单侧切削。这些特点对大螺距加工是十分有利的。
复杂螺纹循环动作和程序格式有很多种,图6为其中一种循环方式的示意图,其程序段可写为:
N-- G⊿⊿ X— Z— I— D— F— A— LF
其中:G⊿⊿为该循环方式的指令代码;X、Z为C点的绝对坐标值;I为螺纹深度;D为第一次循环的切深;A为螺纹牙形角(如60°)。
螺纹深度I减去精加工余量a(0.1~0.6mm)为粗加工总余量。
粗加工余量 = I - a
每次粗切余量是递减的,递减规律决定于数控系统的内部程序。现举两种递减算法的例子:
(1)如图6,当程序给定第一次粗切深D后,第二次及以后的每次总切深顺次为:
D1=D, D2=√D, D3=√D, D4=2D,……。
即每次的粗切深顺次为:D, D(√-1), D(√-√),D(2-√),……。
(2)德国“西门子”3T系统,数控系统给定粗切次数n,则第一次粗切深为D:
D = 2(I-a)/(n 1)
每次的切深为:
D, D-d, D-2d, D-3d, ……。
其中:d=D/n, n为切削次数。