二年级数学口算实用技巧，打好小学数学基础！
●阅读应当成为吸引学生爱好的最重要的发源地。我的教育信念的真理之一，便是无比相信书的教育力量。——苏霍姆林斯基
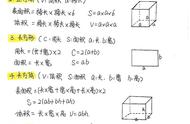
1.凑整法
凑整法就是根据式题的特征，应用定律和性质使运算数据“凑整”。
１、加法凑整
例：32 15 8
原式=32 8 15=40 15=55
几个数相加，如果有几个数相加能凑成整十的数，可以调换加数的位置，再把几个数相加。
2、减法凑整
例：50－13－7
原式=50－（13 7）=50－20=30
从一个数里连续减去几个数，如果减数的和能凑成整十的数，可以把减数先加后再减。
3、乘法凑整
例1：25×14×4
原式=25×4×14=100×14=1400
先熟记25×4=100,125×8=1000；碰到25、125这样大的乘数先看看是否可以凑出4、8。
例2：25×32
原式=25×4×8＝10×8＝80
在熟记上面式子的基础上，把题目中的某数“拆开”分别与另一个数运算。
2.巧用乘法分配律
巧用乘法分配律格式为：m(a b)=ma mb
例1: 33×99
原式=33×（100－1）=3300－33=3267
例2: 666×666
原式=333×2×222×3=999×444=（1000－1）×444=444000－444=443556
3.找基准数法
找基准数法就是先把每个数与基准数的差累计起来，再加上基数与项数的积。
例：623＋595＋602＋600＋588
可选择600为基数，原式=600×5 23－5 2－12=3008
4.熟记常用数据
熟记1到20各自然数的平方数，可以有效提高做计算题的速度。
