——数学 物理小品文2022.10.25
吕武民
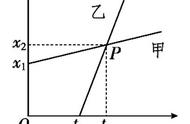
有人说,位移图像的斜率就是速度,所以斜率越大表示的速度就越大。这话前半句没问题,后半句则不妥。那既然前半句没问题,从逻辑上,后半句也不应该有问题的,到底哪里不妥呢?

当然,在质点向x 轴正向运动的“位移—时间图像”中,斜率越大表示的速度就越大是没有问题的。可是,在质点向 x轴负向运动的“位移—时间图像”中,这句话是不对的,因此,笼统地说“斜率越大表示的速度就越大”不妥。
在位移图像中,斜率与速度的定义式相同,却出现了斜率大表示的速度却小的情况。
问题的症结在哪?
速度是矢量,其“正、负”号表示的是方向;
斜率不是矢量,其“正、负”号表示的是大小。
物理中,比较两个矢量的大小,比较的只是大小部分,方向另说;
如果说,“斜率的大小表示的是速度的大小,斜率的正、负表示的是速度的方向”,可以吗?
再说一遍,斜率不是矢量,它除了大小就没别的了,其“正、负”是它大小须臾不可分割的一部分呢,你说完了大小,哪还能剩下什么“正、负”啊!
如果说,位移图像中的直线越陡,表示的速度越大,是可以的;如果说,直线越陡,它的斜率就越大,可以吗?不可以,数学老师表示严重不同意!因为人家的斜率看的是直线与坐标横轴正向夹角的大小。直线越陡这个夹角是越大吗?要看从哪边开始陡了,从锐角开始陡是变大,若从钝角开始陡呢?那个夹角是变小的。
说到这里,似乎感到了物理与数学的不同,各有自己的侧重点,数学是纯理性的,具有更高的概况性;物理则更侧重于实际,运动得快就是快,慢就是慢,至于向南运动还是向北运动,可以另说。而数学则可以把向北的快归纳为向南的慢。数学也可以把“0”叫做一个“数”,而物理上,我们说“内能增加了”,增量就不能是零,否则,那叫骗人,明明没增,你干嘛说增加?……
扯得有点儿远了,还回到原来的问题,在“斜率与速度”的问题上物理和数学到底还能不能和谐?
当然可以。
数学有一个绝好的概念,叫“绝对值”。我们可以说,位移图线斜率的绝对值表示速度的大小,而斜率的正负则表示速度的方向。斜率的绝对值越大,表示的速度就越大。
,