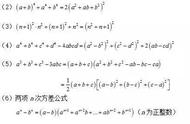因式分解和整式乘法互为逆运算,是初中数学里最重要的恒等式之一。因式分解,是初中数学的重头大戏。如果因式分解没有学好,那么后面分式,一元二次方程等内容就非常的艰难。
很多初学的同学,觉得因式分解好难。因为因式分解灵活多变,技巧性强。但是,真正熟练掌握因式分解方法,原来因式分解一点都不难。
今天,方老师精心挑选了,10道因式分解考试真题,题型常见而且典型,来和大家一起练习。其他的因式分解的类型,方老师后续还会整理发布。欢迎关注,敬请期待。

第0题,通过观察,我们把x²看作一个整体,那么原式就是典型的符合十字交叉相乘分解因式的题型。第一步分解后,一定要检查,分到不能再继续分解为止。
第1题,有平方,有减号。那么首先考虑的是平方差公式。套用平方差公式分解因式后,两个多项式,都符合完全平方公式,继续分解到不能分解为止。

第2题,第3题,这两道题,典型的需要先分组,再分别分解因式的题型。分组的原则是,分组后分别因式分解后,他们有公因式可提。提取公因式,就好。

第4题,一道需要添项的因式分解题。为了套用完全平方公式,先 4x²y²,再-4x²y²。这种方法在配方法解题里经常要用到。同学们自行好好领会,灵活运用。
第5题,这是一个提公因式的因式分解题。但是,我们如果找到多项式的公因式?两个方法,相同的自然是公因式,还有互为相反数的也是公因式。只是,我们在提取公因式的时候,要先讲原来的式子变形。比如,后面那个(b-a)³,我们通过提取一个-1出来,变成了-(a-b)³。这个变形,在很多题型里,经常要用到。

第6题,第7题,这两道题,是需要先去括号,先整式乘法,先合并同类项,之后再进行因式分解的题型。

第8题,和第9题也属于同一种类型。
第8题,我们先把x² x看作成一个整体,先把前面的整式的乘法展开,经过合并同类项后,得到一个关于x² x这个整体的二次三项式。依照十字交叉相乘法因式分解。此题的第一步是关键,很常用。
第9题,我们先把x²-1展开成(x 1)(x-1)后,原式就变成了abcd e的经典题型。我们先把前面的abcd进行分组,分别整式的乘法运算。分组的原则是,整式乘法后,能有相同的部分。比如此题,我们分组分别整式乘法后,两个多项式就有x² 4x的相同部分。然后就和第8题一样了。
,