考试要求,知识梳理
1.通过具体实例,结合5种幂函数函数图象,理解它们的变化规律,了解幂函数;
2.理解二次函数的图象和性质,能用二次函数、方程、不等式之间的关系解决简单问题.
【知识梳理】
1.幂函数
(1)幂函数的定义
(2)常见的5种幂函数的图象
(3)幂函数的性质
①幂函数在(0,+∞)上都有定义;
②当α>0时,幂函数的图象都过点(1,1)和(0,0),且在(0,+∞)上单调递增;
③当α<0时,幂函数的图象都过点(1,1),且在(0,+∞)上单调递减.
2.二次函数
(1)二次函数解析式的三种形式:
一般式:f(x)=ax2+bx+c(a≠0).
顶点式:f(x)=a(x-m)2+n(a≠0),顶点坐标为(m,n).
零点式:f(x)=a(x-x1)(x-x2)(a≠0),x1,x2为f(x)的零点.
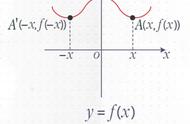
(2)二次函数的图象和性质


【微点提醒】
1.二次函数的单调性、最值与抛物线的开口方向和对称轴及给定区间的范围有关.