敲重点啦!
1.灵活应用幂的乘法运算法则,注意每一步的依据,防止符号上的错误。2.牢牢掌握单项式,多项式的运算法则,多项式与多项式相乘,第一步要先进行整理,在用一个多项式去乘另一个多项式时,要“依次”进行,不重复,不遗漏。3.整式乘法的化简求值,要多进行习题练习,熟练把握做题方法。01
同底数幂的乘法逆应
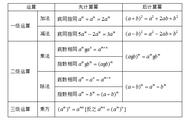
1.同底数幂乘法:
底数不变,指数相加;
2. 同底数幂的逆运用:
题型 1:将计算中的指数相加拆分
幂的乘方逆应用
1.幂的乘方运算:
底数不变,指数相乘;
2. 幂的乘方逆运算:
特点:乘积→乘方;单个指数→多个指
题型 1:将计算中的单个指数拆分多个指数相乘;
题型 2:比较幂的大小 —— 化为同底数或者同指数;
03
积的乘方逆应用
1.积的乘方运算:
因式拆分,分别乘方;
2. 积的乘方逆运算:
方法:能合并,好凑整,优先结合,化简计算
题型 1:指数相同直接优先结合;
题型 2:底数好结合,化为同指数优先结合;
2
整式的乘法
01
单项式x单项式
单项式与单项式相乘:
把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式;
口诀:系乘系,同底幂,单独字母别忘记;
题型:常规计算,注意负号的使用;
02
单项式x多项式
单项式与多项式相乘:
就是用单项式去乘多项式的每一项,再把所得的积相加;
方法:一打多,要求人人过招;
题型:计算化简;
03
多项式x多项式
多项式与多项式相乘:
先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加;
方法:帮派交手,人人过招,有节有礼;
题型 1:常规计算 ;
题型 2:不含某项问题 ;
题型 3:系数对应问题;
3
整式乘法的化简求值
01
利用整式乘法表示图形面积
拆分法
1.利用拆分法表示小面积相加后得到大面积;
2. 利用面积信息得到代数关系;
题型 1:标图表示面积;
题型 2:利用面积解决代数问题
02
整式乘
先利用所学整式计算方法化简,再将具体数值代入求值
题型 1:化简求值的计算;
题型 2:整体思想的应用;
整式、分式、二次根式的化简运算
都是初中学习的重点
贯穿整个初中所学的知识
是我们进行数学运算的基础
让我们打起精神!
一举拿下!