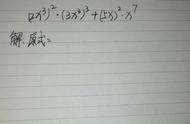第一章 整式的乘除
1. 整式的运算思维导图

2. 幂运算
(1)同底数幂的乘法
运算法则 :同底数幂相乘,底数不变,指数相加。
公式表示 :am * an = am n(m,n都是正整数)
逆应用 :am n = am * an
(2)幂的乘方
运算法则 :幂的乘方,底数不变,指数相乘。
公式表示 :(am)n = amn(m,n都是正整数)
逆应用 :amn = (am)n = (an)m
(3)积的乘方
运算法则 :积的乘方,等于每一个因式乘方的积。
公式表示 :(ab)n = anbn(n是正整数)
逆应用 : anbn = (ab)n
(4)同底数幂的除法
运算法则 :同底数幂相除,底数不变,指数相减。
公式表示 :am ÷ an = am-n(a≠0,m,n都是正整数,且m>n)
(5)零指数幂
运算法则 :
公式表示 :a0 = 1 = (a≠0)
(6)负指数幂
运算法则 :
公式表示 :a-p = 1/ap (a≠0)
3. 整式的乘法
(1)单项式乘以单项式
运算法则 :单项式与单项式相乘,把他们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式。
实质 :分三类乘:a、系数乘系数;b、同底数幂相乘;c、单独一类字母,则连同它的指数照抄。
(2)单项式乘以多项式
运算法则 :单项式与多项式相乘,就是根据分配律用单项式去乘多项式的每一个项,再把所得的积相加。
公式表示 :m(a b c)=ma mb mc (注意各项式之间的符号!)
(3)多项式乘以多项式
运算法则 :多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加。
公式表示 :(m a)(n b)=mn mb an ab (注意各项式之间的符号!)
注意:
①在未合并同类项之前,积的项数等于两个多项式项数的积。
②多项式的每一项包含它前面的符号,确定乘积中每一项的符号时应用:“同号得正,异号得负”。
③运算结果中如果有同类项,则要合并同类项。
4. 乘法公式
(1)平方差公式
语言叙述 :两数和与这两数差的积,等于他们的平方差。
公式表示 :(a b)(a-b)=a2-b2
(2)完全平方公式
语言叙述 :两数和(或差)的平方,等于它们的平方和加上(或减去)这两数积的2倍。
公式表示 :
(a b)2=a2 2ab b2
(a - b)2=a2-2ab b2
5. 整式的除法
(1) 单项式除以单项式
运算法则 :单项式相除,把系数、同底数幂分别相除后,作为商的因式;对于只在被除式里含有字母,则连同它的指数一起作为商的一个因式。
(2) 多项式除以单项式
运算法则 :多项式除以单项式,先把这个多项式的每一项分别除以单项式,再把
所得的商相加。
公式表示 :(a b c)÷ m=a/m b/m c/m
,