一)、由已知想求证
如:有关线段中点的联想
(1)中点 中点=中位线
(2)中点 垂直=等腰(中垂线性质)
(3)中点在Rt⊿斜边上=两个等腰三角形
(4)中点在等腰⊿底边=三线合一
(5)中点倍长,构造8字型全等
(6)三角形中线等分面积
(7)中点坐标公式
如:有关角分线的联想
(1)角分线的性质(常用辅助线三种)
(2)角分线 平行=等腰
(3)两条角平分线交点是内心
(4) 角分线是轴对称变换的标志
二)、由目标想方法
如:证角等
(1)角的计算(三角形内角和、外角定理、互余、互补、对顶、角的和差)
(2)若在一个三角形中,可考虑证等腰;类似的,考虑证平行四边形等;’
(3)若在两个看似全等或相似的三角形中,可考虑证全等或相似;
(4)若属于三线八角,可考虑证平行
(5)圆中,观察同弧所对的圆周角
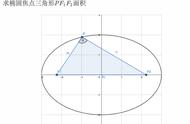
如:求线段最值
(1)代数方法:表示成某个变量的函数,利用函数的最值求解(注意自变量取值);
(2)几何方法:找出动点运动轨迹,用两点间线段最短或三角形三边关系或点到直线垂线段最短等求解。