导数是什么?可能很多人不知道或者早已经还给老师了。但是“微商”这个词,应该很多人都知道,前两年这个词太火。没错,微商就是导数,导数也叫微商,只不过此微商非彼“微商”罢了。
导数的一些概念大概是这样:
1、导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率;
2、若某函数在某一点导数存在,则称其在这一点可导,否则称为不可导。
3、当自变量的增量趋于零时,因变量的增量与自变量的增量之商的极限。也就是当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数。

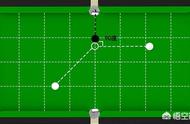
定义很生涩难懂吧,做个形象的比如:有一个函数f(x),它在坐标上显示就是一条弧线(如上图)。关于这个函数是怎样,f(x)你可以认为是一个复杂的y,之所以f里面包含x,就是表明它是随x这个变量变化而变化的。比如函数f(x)=x其实就是y=x,只是这个y=x函数太简单了,在坐标上就是一条直线。
这个函数f(x)的x原来在x0的地方,现在x它变了△x,也就是现在x=x0 △x,比如如现在x=5 0.1=5.1位置。因为f(x)就是y,那么对应的f(x)的变化就是 △y。当△x趋向0的时候,就是△x无穷小0.000…01,这时候 △y/ △x的存在极限数a,那么这个a就是导数了。在数值上看,导数的值是不是就是斜率的数值?

导数的本质是什么,我在网上看到一句话是这样的:导数的本质完全融在它的定义之中,也就是定义中抽象的数学表达式本身就是它最基础的本质!说得非常好。
lim(△x→0) [y(x △x)-y(x)] /△x= lim(△x→0) △y/△x = dy/dx
被定义为y(x) 的导数,所以导数代表的含义要从它的定义及所处领域中寻找。
通过上面可知,导数其实也是极限的问题,它反映的是瞬间自变量(x)极小的变化引起因变量(y)变化的比值的倒数dy/dx,也称为为变化率。我们这个世界万事万物无时无刻都在变化,包括我们的心跳,因此要研究这个世界是如何变化,要掌握它的运动规律,导数就是一个重要的工具了。导数在不同领域中的意义有不同的解释,在数学函数中它表示斜率;在物理位移和时间关系中它是瞬时速度、加速度;在经济学中导数可以分析实际的动态变化,如它可以表示边际成本。这也是导数在实际应用的作用,任何变化的东西,通过导数就可以分析它的瞬态。
明白了导数的概念后,我们看看常见一些导数的求导,从中掌握导数是怎么计算的。
1、y=c,函数等于常数的时候,如f(x)=c,一条平行于x的线,斜率为0,导数肯定等于0了。
2、y=x,y'=lim(△x→0) [(x △x) - x]/△x=lim(△x→0) (2x△x △x)/△x=lim(△x→0) (2x △x),注意,这里△y=(x △x) - x。当△x→0时,lim(△x→0) (2x △x)=2x。

不过以后这种函数记住公式y=x^m,y'=mx^(m-1)直接求导即可,上面计算只是让理解本质过程。
3、x﹢y=1,这是一个隐函数,隐函数求导是直接看出复合函数求导,复合函数求导的结果先外层函数求导,然后乘以内层函数求导结果。令y=f(x),那么y'=f(x)'=f(x)*f(x)]'= f(x)*f(x)' f(x)'*f(x)= 2f(x)*f(x)'= 2yy'。所以,对两边方程两边求导得到结果2x 2yy′=0 。
我们看一下常见的求导公式有哪些,以后求遇到类似的求导直接套用就可以。
1、初等函数的求导公式