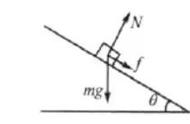
等腰三角形三线合一。
今天我们来看这样一道题:在直角三角形ABC和直角三角形BCD中,这里有两个直角,然后又告诉我们AB和AC相等,并且CD等于5,这条线段等于5。最后告诉我们ABE和ECB相等,让我们求BE的长。
拿到这道题,我们可以看一下题目给的一些条件。这里有一个等腰直角三角形,并且这里还有一个直角,另外告诉我们这两个角相等。这两个角相等是不是意味着BD是不是应该是它的角的角平分线?另外BD和CD又是垂直,垂直就意味着是不会有高的出现。既有角平分线,又有高,我们能想到什么?对三线合一,等腰三角形的三线合一。

所以拿到这两个条件之后,我们就可以知道这题的辅助性应该是怎么做了。我们延长CD,延长BA交于F点,此时我们会发现BD是三角形FBC的一个角平分线,也是它的高线。根据等腰三角形三线合一的推论,我们可以知道BF等于BC,并且BD是CF的一个中线。到这里我们就可以知道DF应该是等于5。

接着往下面看,DF等于5,DC等于5,让我们求BE的长。大家这里可以看到,在三角形ABE中,我们知道这个角是直角,这个边AB和AC是相等的,而且FAC也是90度。也就是说,在三角形ABE和三角形ACF中,我们找到了一组边相等,还找到了一组角相等。

那我们是不是可以试着去证明这两个三角形全等?也就是说,我们只需要再去找另外一组边,或者一组角相等,就可以证明这两个三角形全等。

我们回过来在图形中继续看,这里ABE和CDE这两个三角形组成一个8字形,并且这两处都是直角,这里有一个对等角,那是不是意味着,这个角和这个角应该是相等的,这个角这两个角相等不就是要找的这两组三角形全等的一个条件吗?所以最终可以根据角边角证得这两个三角形是全等的,也就是要求的BE应该是等于CF,也就是两倍的CD,最终就等于10。
,