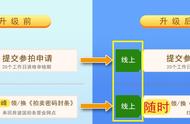
石炭纪巨型蜻蜓,翼展能接近1米|图源网络
虽然大氧化事件的起因尚有争议,但是有理由认为,高氧气浓度促进了这种巨型昆虫的出现,也让我们不禁想如果当今世界的氧浓度增高,会不会也导致巨型生物的出现哈哈哈。但是也正因为氧气浓度高,使得这些巨型昆虫灭绝于一场大火之中。唉!
大体看来,把空气换为纯氧有些疯狂。如果只是提高氧气浓度几个百分点,尚且可以接受,但是对生态系统的影响仍然将十分巨大而需要仔细评估噢。
参考资料:
[1]罗根明,朱祥坤,王水炯,张世红,焦超群.元古宙早期大氧化事件的成因机制与气候生态效应[J].中国科学:地球科学,2022,52(09):1665-1693.
[2]宗普,薛进庄.地质历史时期大气氧含量与生物多样性的协同演变[J].生物学通报,2015,50(04):1-5.
by 小范
Q.E.D.Q8请问像刘慈欣《镜子》里的那样,如果模拟两个完全相同的宇宙起点,结果真的会一样吗?
答:不一定一样,量子力学的不确定性原理使得一切演化过程都变得随机,只能用概率分布来描述。这点我们科普过很多次了,强烈推荐我们这周二发的介绍贝尔不等式的文章[1],里面用通俗的语言介绍了科学家们是如何用实验检验了量子力学不存在局域隐变量,并说明了它是真随机,而不是变量过于复杂导致的伪随机。
我们这里再介绍个诺顿穹顶的模型,它表明即使是在经典物理的框架下,完全相同的初始条件也不一定能推出一样的结果。
一个从诺顿穹顶上滚下的小球 | 图源[2]
2003年,诺顿设想了这么一个神奇的曲面,让一个球从它的顶部下落,它的下落高度h与下落路程r有关系
现在我们把小球静止地放在穹顶上,根据牛顿第二定律和静止的初始条件:
你会发现解出来的演化方程居然多了一个无法确定的常数C,也就是说,这个小球会在t=C时刻下落,但我们没有任何办法确定究竟是哪个时刻下落。这件事还可以反过来想,一个球从下方沿着穹顶向上滚,等它来到穹顶时刚好能稳稳地停住,并静止无限长的时间。顺着这个思路再反回来想,球在穹顶从静止变成下落的时刻是无法确定的。
其实归根结底,这是因为牛顿运动定律对应数学上的二阶微分方程,我们一般认为它加上初位置和初速度两个初始条件就可以确定一个唯一解。但严格来说,这要求微分方程满足Lipschitz条件,它是一个对函数光滑性更严格的条件,而诺顿构造的这个穹顶正好不满足这个条件。
参考资料:
[1]想弄清楚爱因斯坦都搞错的诺奖理论?抓紧来一场量子赌博!
[2]John D. Norton. The Dome
by 牧羊
Q.E.D.
#本期答题团队
霜白、乐在心中、藏痴、云开叶落、小范、牧羊