如何用末影之眼百分百找到要塞（怎么用末影之眼传送自己的位置） - 原点资讯

现在我们从数学的角度，分析一下这种方法的原理。首先建立一个平面直角坐标系，用来模拟的Minecraft的世界位置，假设Steve出生在点A处，丢出一颗末影珍珠，记落地点为A’。再随机走到B点，重复操作，记作点B’。

根据两点确定一条直线的定律，可以通过4点确定2条直线。又因为在同一平面中，不平行的两条直线一定相交。据此就可以轻松地画出交点P，这就是要塞的位置。

如何用末影之眼百分百找到要塞,怎么用末影之眼传送自己的位置(1)

[Pv.1-1] 利用交点确定要塞坐标

刚才讨论的是几何原理。如果给这些点代入具体的数据，用联立一次函数解方程的方法，就能够计算出要塞的坐标了。得到4个点坐标。代入解析式得到ya和yb。最后联立函数，计算出交点的坐标，要塞位于(40.8，40)。

如何用末影之眼百分百找到要塞,怎么用末影之眼传送自己的位置(2)

[Pv.1-2] 联立一次函数解方程

但在实际测距的过程中，由于不可避免的角度偏差，并且要塞位置偏远，这使得误差大的足以让你找不到要塞在哪。此时，就可以用3次测距取平均值的方法大大缩短误差。如下图所示测距三次，由于误差原因交于3点a.b.c。因为不在同一条直线上，首尾相接的三条线段构成三角形，故将交点的封闭图形视作三角形。

为了求到最精确的点，应该先画出该三角形的水平宽和铅锤高。取宽和高的中垂线，交三角形内部于点Q。Q即为要塞坐标。(即三角形外接矩形的重心)

同样代入具体数据，用代数法求出精确坐标。水平宽的中点为(0.5*(50 65),35)，铅锤高的中点为(65,0.5*(35 60))。化简得(57.5,35) (65,47.5)，最终点Q为(57.5,47.5)。

如何用末影之眼百分百找到要塞,怎么用末影之眼传送自己的位置(3)

[Pv.1-3] 误差的确定算法

但三次测距本身需要解6次二元一次方程组，再确定宽高平均值，并且数据都保留了3位小数，计算量非常大，很容易算错。这里up主采用了C语言编程的方法，实现了计算的自动化。下面是程序的完整代码。

#include <stdio.h> //I/O标准输入输出流 #include <math.h> //开平方&根号操作 int main(void){ /***********************数据定义区域***********************/ int i,j; //循环(无实意) double p; //用于稍后的排序 double x[6],y[6]; //指测量坐标共测量6个点 double k[3],b[3]; //指函数参数共有3个一次函数 double Rx[3],Ry[3]; //指交点坐标 3个函数共有3个交点 double RL,RH; //指构成三角形的水平宽铅锤高坐标(结果) /***********************用户交互区域***********************/ printf("Minecraft 求解地牢坐标工具v1.2 (制作：b站小泠君丶)\n\n"); printf("<现在，请输入你的测量数据>\n\n"); j=-1; for(i=1;i<4;i ){ //循环3次获取坐标位置 j ; printf("输入第%d次的原地x坐标：",i); scanf("%lf",&x[j]); printf("输入第%d次的原地y坐标：",i); scanf("%lf",&y[j]); j ; printf("输入第%d次的末影之眼x坐标：",i); scanf("%lf",&x[j]); printf("输入第%d次的末影之眼y坐标：",i); scanf("%lf",&y[j]); printf("\n"); } /**********************求并解函数解析式********************/ j=0; for(i=0;i<3;i ){ k[i]=(y[j 1]-y[j])/(x[j 1]-x[j]); //求解系数k b[i]=y[j]-(x[j]*k[i]); //求解常数项b j =2; } for(i=0;i<2;i ){ Rx[i]=(b[i]-b[i 1])/(k[i 1]-k[i]); //求解交点(1-2/2-3) Ry[i]=Rx[i]*k[i] b[i]; //y=kx b } Rx[2]=(b[2]-b[0])/(k[0]-k[2]); //求解交点(1-3) Ry[2]=Rx[2]*k[2] b[2]; /***********************误差确认区域***********************/ //排序算法排列三个交点Rx与Ry p作为交换变量 if(Rx[0]<Rx[1]){ p=Rx[0]; Rx[0]=Rx[1]; Rx[1]=p; }if(Rx[0]<Rx[2]){ p=Rx[0]; Rx[0]=Rx[2]; Rx[2]=p; }if(Rx[1]<Rx[2]){ p=Rx[1]; Rx[1]=Rx[2]; Rx[2]=p; }if(Ry[0]<Ry[1]){ p=Ry[0]; Ry[0]=Ry[1]; Ry[1]=p; }if(Ry[0]<Ry[2]){ p=Ry[0]; Ry[0]=Ry[2]; Ry[2]=p; }if(Ry[1]<Ry[2]){ p=Ry[1]; Ry[1]=Ry[2]; Ry[2]=p; } /*此时大小排列：Rx[0]>Rx[1]>Rx[2] 即L=Rx[0]-Rx[2];*/ RL=0.5*(Rx[0] Rx[2]); RH=0.5*(Ry[0] Ry[2]); /***********************用户交互区域***********************/ printf("成功计算！地牢坐标位于（%lf,%lf）处！\n\n",RL,RH); printf("----------------调试信息-----------------\n"); printf("确认输入：第一次 (%.2lf,%.2lf) (%.2lf,%.2lf)\n",x[0],y[0],x[1],y[1]); printf("确认输入：第二次 (%.2lf,%.2lf) (%.2lf,%.2lf)\n",x[2],y[2],x[3],y[3]); printf("确认输入：第三次 (%.2lf,%.2lf) (%.2lf,%.2lf)\n",x[4],y[4],x[5],y[5]); printf("确认解析：y=%.2lfx% .2lf y=%.2lfx% .2lf y=%.2lfx% .2lf\n",k[0],b[0],k[1],b[1],k[2],b[2]); printf("确认交点：(%.2lf,%.2lf) (%.2lf,%.2lf) (%.2lf,%.2lf)\n",Rx[0],Ry[0],Rx[1],Ry[1],Rx[2],Ry[2]); printf("\n按<任意键>退出本程序."); getch(); return 0; }

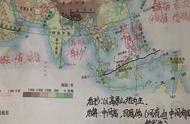
应用上面讲过的测距和提高精度，就可以很精确的计算要塞位置。但要真正了解末影定位的原理，就需要先了解要塞的生成算法。首先，主世界中会生成128个地牢。分布规律是这样的，以出生点作为中心O，依次向外做出8个圆心为出生点的圆环。每个圆环的宽度为1280米，相邻两个环间间隔3072m。圆心O距第一环为1408米。每个环上都会随机生成不等数量的地牢。随机模拟分布情况，类似于下图所示，标定的黄点就是要塞。这么多要塞会导致什么问题呢？答案是会导致测定时没有指向同一位置。

如何用末影之眼百分百找到要塞,怎么用末影之眼传送自己的位置(4)