(1)二进制转十进制
方法:“按权展开求和”
【例】:

规律:个位上的数字的次数是0,十位上的数字的次数是1,......,依次递增,而十
分位的数字的次数是-1,百分位上数字的次数是-2,......,依次递减。
注意:不是任何一个十进制小数都能转换成有限位的二进制数。
(2)十进制转二进制
· 十进制整数转二进制数:“除以2取余,逆序排列”(除二取余法)
【例】:

89÷2 ……1,44÷2 ……0,22÷2 ……0,11÷2 ……1,5÷2 ……1,2÷2 ……0,1
十进制小数转二进制数:“乘以2取整,顺序排列”(乘2取整法)
【例】: (0.625)10= (0.101)2
0.625X2=1.25 ……1
0.25 X2=0.50 ……0
0.50 X2=1.00 ……1
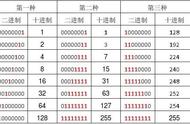
十进制1至128的二进制表示:
0=0
1=1
2=10
3=11
4=100
5=101
6=110
7=111
8=1000
9=1001
10=1010
11=1011
12=1100
13=1101
14=1110
15=1111
16=10000
17=10001
18=10010
19=10011
20=10100
21=10101
22=10110
23=10111
24=11000
25=11001
26=11010
27=11011
28=11100
29=11101
30=11110
31=11111
32=100000
33=100001
34=100010
35=100011
36=100100
37=100101
38=100110
39=100111
40=101000
41=101001
42=101010
43=101011
44=101100
45=101101
46=101110
47=101111
48=110000
49=110001
50=110010
51=110011
52=110100
53=110101
54=110110
55=110111
56=111000
57=111001
58=111010
59=111011
60=111100
61=111101
62=111110
63=111111
64=1000000
65=1000001
66=1000010
67=1000011
68=1000100
69=1000101
70=1000110
71=1000111
72=1001000
73=1001001
74=1001010
75=1001011
76=1001100
77=1001101
78=1001110
79=1001111
80=1010000
81=1010001
82=1010010
83=1010011
84=1010100
85=1010101
86=1010110
87=1010111
88=1011000
89=1011001
90=1011010
91=1011011
92=1011100
93=1011101
94=1011110
95=1011111
96=1100000
97=1100001
98=1100010
99=1100011
100=1100100
101=1100101
102=1100110
103=1100111
104=1101000
105=1101001
106=1101010
107=1101011
108=1101100
109=1101101
110=1101110
111=1101111
112=1110000
113=1110001
114=1110010
115=1110011
116=1110100
117=1110101
118=1110110
119=1110111
120=1111000
121=1111001
122=1111010
123=1111011
124=1111100
125=1111101
126=1111110
127=1111111
128=10000000
十进制负数转二进制:“先取正数的二进制值,再取反,加1”
【例】:(-31)10 = (1)2
31的二进制数为11111,取反00000,加1得1。
与八进制二进制数转换成八进制数:从小数点开始,整数部分向左、小数部分向右,每3位为一组用一位八进制数的数字表示,不足3位的要用“0”补足3位,就得到一个八进制数。
八进制数转换成二进制数:把每一个八进制数转换成3位的二进制数,就得到一个二进制数。
八进制数字与十进制数字对应关系如下:
000 -> 0 | 004-> 4 | 010=8
001 -> 1 |005 -> 5| 011=9
002 -> 2 |006 -> 6 | 012=10
003 -> 3 |007 -> 7 | 013=11
【例】:将八进制的37.416转换成二进制数:
3 7 . 4 1 6
011 111 .100 001 110
即:(37.416)8 =(11111.10000111)2
【例】:将二进制的10110.0011 转换成八进制:
0 1 0 1 1 0 . 0 0 1 1 0 0
2 6 . 1 4
即:(10110.0011)2 = (26.14)8

二进制数转换成十六进制数:二进制数转换成十六进制数时,只要从小数点位置开始,向左或向右每四位二进制划分一组(不足四位数可补0),然后写出每一组二进制数所对应的十六进制数码即可。
十六进制数转换成二进制数:把每一个十六进制数转换成4位的二进制数,就得到一个二进制数。
十六进制数字与二进制数字的对应关系如下:
0000 -> 0 0100 -> 4 1000 -> 8 1100 -> C
0001 -> 1 0101 -> 5 1001 -> 9 1101 -> D
0010 -> 2 0110 -> 6 1010 -> A 1110 -> E
0011 -> 3 0111 -> 7 1011 -> B 1111 -> F
【例】:将十六进制数5DF.9 转换成二进制:
5 D F . 9
0101 1101 1111 .1001
即:(5DF.9)16 =(10111011111.1001)2{十六进制怎么会有小数点}
【例】:将二进制数1100001.111 转换成十六进制:
0110 0001 . 1110
6 1 . E
即:(1100001.111)2 =(61.E)16
与十进制的区别
二进制与十进制的区别在于数码的个数和进位规律有很大的区别,顾名思义,二进制的计数规律为逢二进一,是以2为基数的计数体制。10这个数在二进制和十进制中所表示的意义完全不同,在十进制中就是我们通常所说的十,在二进制中,其中的一个意义可能是表示一个大小等价于十进制数2的数值。
仿照例题1.3.1,我们可以将二进制数10表示为:10=1×2^1 0×2^0

十进制与二进制的关系
一般地,任意二进制数可表示为:
例题 1.3.2 试将二进制数(01010110)B转换为十进制数。
解:将每一位二进制数乘以位权后相加便得相应的十进制数
在数字电子技术和计算机应用中,二值数据常用数字波形来表示。使用数字波形可以使得数据比较直观,也便于使用电子示波器进行监视。

用二进制数的数字编码波形图
图中给出了四个二进制波形。看这种二进制波形图时,我们应当沿着图中虚线所示的方向来看,即使图中没有标出虚线(一般都没有标出),也要想象出虚线来。其中在每一个波形上方的数字表示了与波形对应的位的数值,最后一行则是相应的十进制数 ,其中LSB是英文Least Significant Bit的缩写,表示最低位,MSB是Most Significant Bit的缩写,表示二进制数的最高位。显然,这是一组4位的二进制数,总共有16组,最左边的二进制数为0000,最上边的波形代表二进制数的最低位,也就是通常在十进制数中我们所说的个位数,最下面的是最高位。图中最右边的二进制数为1111,对应的十进制数为15。再来看看对应于十进制数5的二进制数是多少呢?是0101,对了,读数的顺序是从下往上。