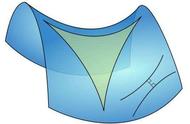
现在我们让B再回到圆心处,接下来的工作是,我们要去测量这个转动圆盘的半径和周长,我们作为圆盘以外的观察者去测量圆盘的半径和周长所获得的数值,和B在圆盘中心测量所获得的数值一样,因为我们都相对于圆盘是静止的。
但是A在圆盘的边缘跟着圆盘转动,他测量出来的圆盘的周长却比我们测量出来的周长要长,因为A手中的尺子在我们看来发生了洛伦兹收缩,所以他测量周长的时候就会导致,在我们看来他需要多量几次才能量完一周,而我们虽然看到了圆盘边缘的周长也发生了洛伦兹收缩,但是我们尺子没有变化。
所以A测量出来的周长,要大于我们测量出来的周长。
如果利用A测量出来的周长除以半径,我们就会发现,结果大于2Π,这跟我们平面上的圆不一样。

平面就代表了二维的平直空间,这说明这个圆本身不在一个平直的空间中,或者说不在欧式空间中,而是处在了弯曲的罗氏空间中。
爱因斯坦通过这个思想实验,确定了有引力的地方时空结构不再是平直的。所以断定引力并不存在,而是时空的弯曲,我们看到的引力作用,其实是一种时空的几何效应。
既然爱因斯坦发现了引力的本质,就是时空的弯曲,他就需要对弯曲的时空进行几何描述,而此时黎曼的球面几何已经静静躺在那里,等在爱因斯坦这位知音。
相信你已经从上文看到了三种几何:欧式几何、罗氏几何、黎曼几何。这三种几何是啥意思,有啥关系?
这是我们下节课的内容。