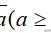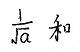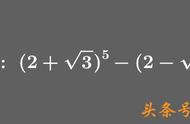第十六章 二次根式
知识点一:二次根式的概念
【知识要点】
二次根式的定义:形如
的式子叫二次根式,其中
叫被开方数,只有当
是一个非负数时,
才有意义.
【典型例题】
题型一:二次根式的判定
【例1】下列各式1)
,
其中是二次根式的是_________(填序号).
题型二:二次根式有意义
【例2】若式子
有意义,则x的取值范围是 .
题型三:二次根式定义的运用
【例3】若y=
2009,则x y=
解题思路:式
子
(a≥0),
,y=2009,则x y=2014
题型四:二次根式的整数与小数部分
已知a是
整数部分,b是
的小数部分,求
的值。
若
的整数部分是a,小数部分是b,则
。
若
的整数部分为x,小数部分为y,求
的值.
知识点二:二次根式的性质
【知识要点】
1. 非负性:
是一个非负数.
注意:此性质可作公式记住,后面根式运算中经常用到.
2.
.
注意:此性质既可正用,也可反用,反用的意义在于,可以把任意一个非负数或非负代数式写成完全平方的形式:
3.
注意:(1)字母不一定是正数.
(2)能开得尽方的因式移到根号外时,必须用它的算术平方根代替.
(3)可移到根号内的因式,必须是非负因式,如果因式的值是负的,应把负号留在根号外.
4. 公式
与
的区别与联系
(1)
表示求一个数的平方的算术根,a的范围是一切实数.
(2)
表示一个数的算术平方根的平方,a的范围是非负数.
(3)
和
的运算结果都是非负的.
【典型例题】
题型一:二次根式的双重非负性
【例4】若
则
.
题型二:二次根式的性质2 (公式
的运用)
【例5】 化简:
的结果为( )
A、4—2a B、0 C、2a—4 D、4
题型三:二次根式的性质3 (公式
的应用)
【例6】已知
,则化简
的结果是
A、
B、
C、
D、
知识点三:最简二次根式和同类二次根式
【知识要点】
1、最简二次根式:
(1)最简二次根式的定义:①被开方数是整数,因式是整式;②被开方数中不含能开得尽方的数或因式.
2、同类二次根式(可合并根式):
几个二次根式化成最简二次根式后,如果被开方数相同,这几个二次根式就叫做同类二次根式,即可以合并的两个根式。
【典型例题】
【例7】在根式1)
,最简二次根式是( )
A.1) 2) B.3) 4) C.1) 3) D.1) 4)
解题思路:掌握最简二次根式的条件。
知识点四:二次根式计算——分母有理化
【知识要点】
1.分母有理化
定义:把分母中的根号化去,叫做分母有理化。
2.有理化因式:
两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,就说这两个代数式互为有理化因式。有理化因式确定方法如下:
①单项二次根式:利用
来确定,如:
,
,
与
等分别互为有理化因式。
②两项二次根式:利用平方差公式来确定。如
与
,
,
分别互为有理化因式。
3.分母有理化的方法与步骤:
①先将分子、分母化成最简二次根式;
②将分子、分母都乘以分母的有理化因式,使分母中不含根式;
③最后结果必须化成最简二次根式或有理式。
【典型例题】
【例8】 把下列各式分母有理化
(1)
(2)
(3)
(4)
【例9】把下列各式分母有理化
(1)
(2)
(3)
(4)
【例10】把下列各式分母有理化:
(1)
(2)
(3)
小结:一般常见的互为有理化因式有如下几类:
①
与
; ②
与
;
③
与
; ④
与
.
知识点五:二次根式计算——二次根式的乘除
【知识要点】
1.积的算术平方根的性质:积的算术平方根,等于积中各因式的算术平方根的积。
=
·
(a≥0,b≥0)
2.二次根式的乘法法则:两个因式的算术平方根的积,等于这两个因式积的算术平方根。
·
=
.(a≥0,b≥0)
3.商的算术平方根的性质:商的算术平方根等于被除式的算术平方根除以除式的算术平方根
=
(a≥0,b>0)
4.二次根式的除法法则:两个数的算术平方根的商,等于这两个数的商的算术平方根。
=
(a≥0,b>0)
注意:乘、除法的运算法则要灵活运用,在实际运算中经常从等式的右边变形至等式的左边,同时还要考虑字母的取值范围,最后把运算结果化成最简二次根式.
【典型例题】
【例11】化简
(1)
(2)
(3)
【例12】计算(1)
(2)
(3)
(4)
知识点六:二次根式计算——二次根式的加减
【知识要点】
需要先把二次根式化简,然后把被开方数相同的二次根式(即同类二次根式)的系数相加减,被开方数不变。
注意:对于二次根式的加减,关键是合并同类二次根式,通常是先化成最简二次根式,再把同类二次根式合并.但在化简二次根式时,二次根式的被开方数应不含分母,不含能开得尽的因数.
【典型例题】
【例13】计算
(1)
; (2)
;
【例14】 (1)
(2)
知识点七:二次根式计算——二次根式的混合计算与求值
【知识要点】
1、确定运算顺序;
2、灵活运用运算定律;
3、正确使用乘法公式;
4、大多数分母有理化要及时;
5、在有些简便运算中也许可以约分,不要盲目有理化;
【典型习题】
1、
2、 (2 4-3)
【例15】 1.已知:
,求
的值.
知识点八:根式比较大小
【知识要点】
1、根式变形法 当
时,①如果
,则
;②如果
,则
。
2、平方法 当
时,①如果
,则
;②如果
,则
。
3、分母有理化法 通过分母有理化,利用分子的大小来比较。
4、分子有理化法 通过分子有理化,利用分母的大小来比较。
5、倒数法
6、媒介传递法 适当选择介于两个数之间的媒介值,利用传递性进行比较。
7、作差比较法
在对两数比较大小时,经常运用如下性质:①
;②
8、求商比较法
9、它运用如下性质:当a>0,b>0时,则:①
; ②
【典型例题】
【例16】 比较
与
的大小。(用两种方法解答)
【例17】比较
与
的大小。
一 元 二 次 方 程
一、知识结构:
一元二次方程
二、考点精析
考点一、概念
(1)定义:①只含有一个未知数,并且②未知数的最高次数是2,这样的③整式方程就是一元二次方程。
(2)一般表达式:
⑶难点:如何理解 “未知数的最高次数是2”:
①该项系数不为“0”;
②未知数指数为“2”;
③若存在某项指数为待定系数,或系数也有待定,则需建立方程或不等式加以讨论。
典型例题:
例1、下列方程中是关于x的一元二次方程的是( )
A、
B、
C、
D、
变式:当k 时,关于x的方程
是一元二次方程。
例2、方程
是关于x的一元二次方程,则m的值为 。
考点二、方程的解
⑴概念:使方程两边相等的未知数的值,就是方程的解。
⑵应用:利用根的概念求代数式的值;
典型例题:
例1、已知
的值为2,则
的值为 。
考点三、解法
⑴方法:①直接开方法;②因式分解法;③配方法;④公式法
⑵关键点:降次
类型一、直接开方法:
※※对于
,
等形式均适用直接开方法
典型例题:
例1、解方程:
=0;
例2、若
,则x的值为 。
类型二、因式分解法:
※方程特点:左边可以分解为两个一次因式的积,右边为“0”,
※方程形式:如
,
,
典型例题:
例1、
的根为( )
A
B
C
D
例2、若
,则4x y的值为 。
例3、方程
的解为( )
A.
B.
C.
D.
例4、解方程:
例5、已知
,则
的值为 。
类型三、配方法
※在解方程中,多不用配方法;但常利用配方思想求解代数式
的值或极值之类的问题。
典型例题:
例1、 试用配方法说明
的值恒大于0。
例2、 已知x、y为实数,求代数式
的最小值。
例3、 已知
为实数,求
的值。
例4、 分解因式:
类型四、公式法
⑴条件:
⑵公式:
,
典型例题:
例1、选择适当方法解下列方程:
⑴
⑵
⑶
例2、在实数范围内分解因式:
(1)
;(2)
. ⑶
说明:①对于二次三项式
的因式分解,如果在有理数范围内不能分解,一般情况要用求根公式,这种方法首先令
=0,求两根,再写成
=
.②分解结果是否把二次项系数乘进括号内,取决于能否把括号内的分母化去.
类型五、 “降次思想”的应用
⑴求代数式的值; ⑵解二元二次方程组。
典型例题:
例1、 已知
,求代数式
的值。
例2、如果
,那么代数式
的值。
说明:解二元二次方程组的具体思维方法有两种:①先消元,再降次;②先降次,再消元。但都体现了一种共同的数学思想——化归思想,即把新问题转化归结为我们已知的问题.
考点四、根的判别式
根的判别式的作用:
①定根的个数;②求待定系数的值;③应用于其它。
典型例题:
例1、若关于
的方程
有两个不相等的实数根,则k的取值范围是 。
例2、关于x的方程
有实数根,则m的取值范围是( )
A.
B.
C.
D.
例3、已知关于x的方程
(1)求证:无论k取何值时,方程总有实数根;
(2)若等腰
ABC的一边长为1,另两边长恰好是方程的两个根,求
ABC的周长。
例4、已知二次三项式
是一个完全平方式,试求
的值.
例5、
为何值时,方程组
有两个不同的实数解?有两个相同的实数解?
考点五、方程类问题中的“分类讨论”
典型例题:
例1、关于x的方程
⑴有两个实数根,则m为 ,⑵只有一个根,则m为 。
例2、 不解方程,判断关于x的方程
根的情况。
例3、 如果关于x的方程
及方程
均有实数根,问这两方程
是否有相同的根?若有,请求出这相同的根及k的值;若没有,请说明理由。
考点六、应用解答题
⑴“碰面”问题;⑵“复利率”问题;⑶“几何”问题;
⑷“最值”型问题;⑸“图表”类问题
考点七、根与系数的关系
⑴前提:对于
而言,当满足①
、②
时,
才能用韦达定理。⑵主要内容:
⑶应用:整体代入求值。典型例题:
例1、已知一个直角三角形的两直角边长恰是方程
的两根,则这个直角三角形的斜边是( )
A.
B.3 C.6 D.
例2、已知关于x的方程
有两个不相等的实数根
,
(1)求k的取值范围;
(2)是否存在实数k,使方程的两实数根互为相反数?若存在,求出k的值;若不存在,请说明理由。
例3、小明和小红一起做作业,在解一道一元二次方程(二次项系数为1)时,小明因看错常数项,而得到解为8和2,小红因看错了一次项系数,而得到解为-9和-1。你知道原来的方程是什么吗?其正确解应该是多少?
例4、已知
,
,
,求
变式:若
,
,则
的值为 。
例5、已知
是方程
的两个根,那么
.
针对练习:
1、解方程组
2.已知
,
,求
的值。
3、已知
是方程
的两实数根,求
的值。
,