一、前言
等差数列之前已经讲了,如果没有看的读者可以去看看之前作者发布的文章,今天要讲的就是等比数列,很多高中生觉得自己理解了等比数列,但事实上真的理解正确了吗?
二、等比数列定义
等比数列学习,肯定必须先要学习等比数列的定义,才能够更好的理解,后续的知识点,那到底什么是等比数列?
一般地,如果一个数列从第二项起,每一项与它的前一项的比等于同一常数,那么这个数列就是等比数列。
这个常数叫做等比数列的公比,并且这个公比通常都是用q来表示的。
三、定义表达式
等比数列的表达式:

这就是等比数列由定义写出来的数学表达式,除此之外,还有以下表达式:

这些公式都是由定义推出来的,但是当使用后面那个表达式的时候,必须要跟上n的取值范围。
四、等比数列的通项公式
由等比数列的定义是可以用首项与公比,来表示等比数列的所有的项。
这样就可以推出来等比数列的通项公式:
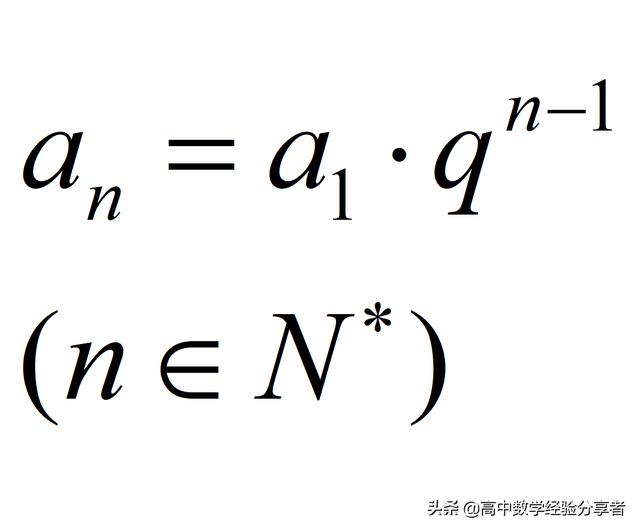
求解等比数列的通项公式就需要知道等比数列的首项与公比才可以求解,也就是当题目中给的条件不够就需要进行转化,用首项和公比进行表示。
五、等比中项
当a,b,c三个数成等比数列的时候,那么b就叫做a与c的等比中项,此时满足等比中项的要求:

注意:
1)首先要明白并不是任意的两项就有等比中项,只有当这两项同号时,才会有等比中项,并且这个等比中项有两个,并且互为相反数。
2)并且要牢牢记住,在等比数列中,除去首尾两项之外,任何一项都是前后两项的等比中项。
批注:
读者有什么不懂的可以留言,想要知道什么高中解题经验可以给作者留言啊!
关注!关注!关注!重要事情说三遍
,














